8パズル/15パズルを解く(1) 幅優先探索
8パズル/15パズルとは何か
15パズルとは,下のような見た目をしたパズルのことである.解く人は,空いているマスに数字をスライドさせる操作を繰り返し(例えば,下の画像の状況では,13の右移動と,7の下移動が許容される),数字を左上から右下に向かって昇順に並べ,右下の隅を空白にする必要がある.
8パズルは15パズルの簡略版で,盤面のサイズを3×3とし,数字を1から8までに減らしたものである.
幅優先探索(BFS)のアルゴリズム
このようなパズルを解くための基本となるのが,グラフ上の二節点の最短距離を求めるのに使用される,幅優先探索(BFS)である.
BFSには,キュー(queue)という,先入れ先出し(First in, First out)のデータ構造を利用する.キューには,要素を末尾に追加する動作pushと,先頭の要素を削除する動作popが定義されており,それらが高速に行われるという特徴がある.
以下にBFSのアルゴリズムを示す.ただし,$${V}$$は頂点集合,$${E}$$は隣接リスト,$${v_s}$$は始点を表している.

パズルとBFS
BFSを活用して8パズル/15パズルを解くには,このパズルをグラフの探索問題に帰着させればよい.
いま,パズルの盤面をグラフの節点として捉えることにする.そして,ある節点$${v}$$と隣接する節点の集合$${E[v]}$$は,盤面$${v}$$から一手で移動可能な盤面の集合であるとしよう.このように考えれば,始点から目標まで辿ったときの「深さ」が必要な手数に対応し,その過程で通った盤面こそが,解法であるとみなせるだろう.
しかし,問題は,いかにして隣接リスト$${E}$$を取得するかという点にある.8パズルの盤面は約18万通りであり,18万の盤面すべてについて隣接節点を求めるのは(それが必要となることもあるかもしれないが),多くの場合で無駄が多い.
そこで,$${E}$$(および$${d}$$)は,連想配列によって実現したい.連想配列を活用すれば,訪問した節点について,適宜隣接する節点の情報を追加できるので効率的だ.また,連想配列は,特定のキーの情報に対するアクセスが高速であるという点で,多次元リストに勝っている.
BFSの欠点
しかし,BFSは想定しうる可能性(グラフの節点,パズルの盤面)を網羅的に探索するので,その可能性があまりに膨大な場合,時間がかかりすぎてしまい,有効でない.たとえば,8パズルの盤面数は18万程度だから,BFSを行ったとしても,現実的な時間で解を発見することができる.一方,15パズルの盤面数は10兆を超えるので,15パズルについてBFSを行うのは非現実的であると考えられる.そこで,今回は8パズルのみを対象としたい.
なお,この問題を解決するためには,例えば「正解の盤面に近づきそうなものを優先的に探索する」といったような戦略が考えられる.その発想を取り入れたのがA*探索だが,A*探索を活用する場合,「正解の盤面に近づきそうなもの」の評価方法が問題となる.
Pythonによる実装
Pythonを用いて8パズルをBFSで解くクラスを定義する.つまり,
sb = Solver8BFS()
puzzle1 = np.array([
[1, 3, 0],
[4, 6, 2],
[7, 8, 5]
])
sb.solve(puzzle1)といった具合でsolveメソッドを実行することで,解のための最小手数や(必要に応じて)手順などを出力するようなクラス,Solver8BFSを実装したい.言うまでもなく,引数となる二次元配列の各要素は盤上の数字を表し,0はそのマスが空白であることを示している.
予めインポートしておくべきライブラリ等は以下の通り.
import numpy as np
import time
from collections import dequedequeをインポートすることによって,キューをPythonで扱うことができる.(ただし,dequeは両端キューと呼ばれるもので,末尾に対しての追加・削除も高速なデータ構造だから,キューとは少し異なる)
class Solver8BFS:
def getPossibleMove(self, board_t):
# 次に可能な盤面(tupleで表現)のlistを返す
board = np.array(board_t).reshape(3,3)
act = []
ret = []
[r0, c0] = np.array([np.where(board==0)[0][0], np.where(board==0)[1][0]])
if r0 > 0: act.append(np.array([r0-1, c0]))
if r0 < 2: act.append(np.array([r0+1, c0]))
if c0 > 0: act.append(np.array([r0, c0-1]))
if c0 < 2: act.append(np.array([r0, c0+1]))
for [row, col] in act:
cpy = board.copy()
buff = board[row,col]
cpy[r0, c0] = buff
cpy[row,col] = 0
ret.append(tuple(cpy.flatten()))
return ret
def solve(self, puzzle, show=True):
# 動作のメイン部分
start = tuple(puzzle.flatten()) # 初期状態
goal = np.array(range(1,10))
goal[8] = 0
goal = tuple(goal) # 目標盤面
q = deque() # キュー
adj = dict() # 隣接リスト
d = dict() # 深さの記録/探索済みの節点集合
parent = dict() # 親の記録
start_time = time.time() # 時間計測開始
# BFS開始
q.append(start)
d[start] = 0
while len(q) != 0:
b = q.popleft()
if not b in adj:
adj[b] = self.getPossibleMove(b)
for i in adj[b]:
if not i in d:
q.append(i)
d[i] = d[b]+1
parent[i] = b
if i==goal:
break
if goal in d:
break
# BFS終了
t = time.time()-start_time # 時間計測終了
print("start:\n", puzzle)
print("time:", t, "sec")
if not goal in d: # 目標が探索済みにならなかった=失敗
print("failed.")
else:
print("solved!")
trace = []
b = goal
trace.append(b)
while b != start:
b = parent[b]
trace.append(b)
trace.reverse()
print("move:", len(trace)-1)
if show:
for i in range(len(trace)):
print(np.array(trace[i]).reshape(3,3))
print("explored Node:", len(d))getPossibleMove()は,そのときの盤面(board_t)を引数にとって,次の盤面として想定しうる状況を,tupleのlistとして返す.ここで,盤面の表現を(listやndarrayでなく)tupleにしておくことが重要である.BFSの過程で,各盤面(ノード)の隣接関係や深さの情報などは,すべてdict(連想配列)の形で記録されなければならないが,ndarrayやlistをdictのキーとして使用することはできないからだ.予めtupleに変換しておくことで,この問題を回避できる.
solve()はBFSを実践する.BFSの基本的なアルゴリズムや,8パズルへの適用にあたっての留意事項は前に述べた通りである.timeライブラリの機能を利用することで,探索にかかる時間も測定できるようにした.
実行例
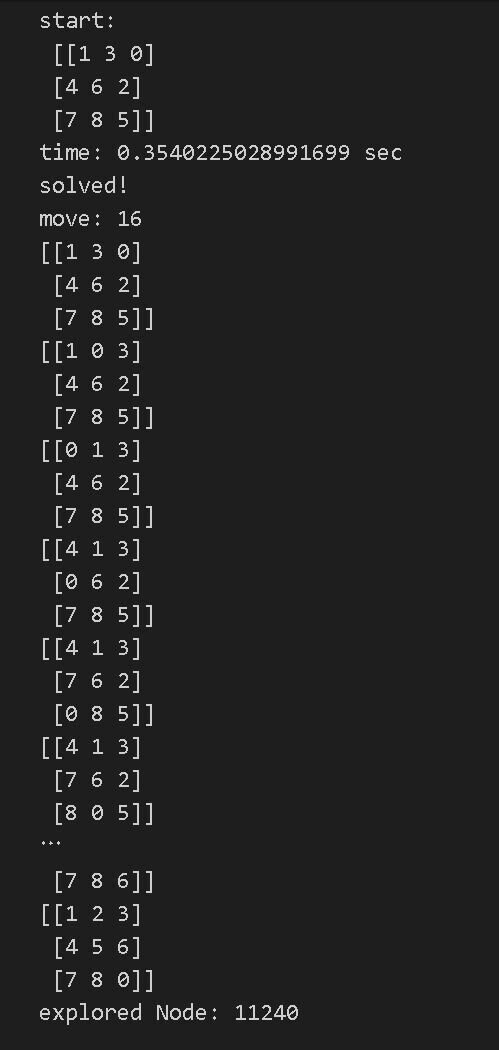
sb = Solver8BFS()
puzzle1 = np.array([
[1, 3, 0],
[4, 6, 2],
[7, 8, 5]
])
sb.solve(puzzle1)上のコードを実行すると,以下のような結果を得る.この盤面から開始すると,目標まで16回の移動が必要で,11240個の節点を訪問することになるようだ.