
ボリンジャー??マジガチ余裕だしw
って言ってみたいですよねー。。。
正直言ってボリンジャー余裕とか絶対に口が裂けても言えないです・・・。まあそこまで言えなくても、ガウス分布(正規分布)は至る所で出てくるので勉強しておいて損はないですよ!!
私は数学も統計学も大好きなのですが、正直ほにゃらら分布ってあまり得意ではないです。。。だってこの場合はPoisson分布でそれはこんな式でこんな性質がある、そしてこの場合は Gauss分布で...とか色々あってややこし過ぎるんです!テキストを読んでもいろんな分布の特徴がまとめられて表になっていているんですが、そんなのを見ても全然頭に入ってきません。なので、まずはGaussianことGauss分布だけでもその特徴を押さえておきましょう!!
Gauss分布って何??
正規分布とも呼びますが、この分布を研究した偉大な科学者をたたえてGauss分布、あるいはGaussianとも呼びます。形はこんな釣鐘状の形をしています。
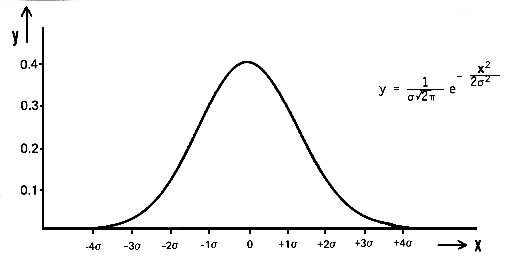
まあ適当な例なのでこのグラフに意味はないのですが、横軸は値、縦軸はその値が起こる頻度と思ってください。
そしてこの形が美しいと思えたあなた!なかなかセンスがあります(笑)実はこのGauss分布って自然科学で欠かせないだけではなく、意外と日常生活にも潜んでいるんですよ。例えば、私はハッキリ言って好きじゃないのですがIQって指標がありますよね。あれも中心の値を100と定義して、その広がりが正規分布になっているみたいです。受験の時の偏差値なんかもそうですね。他にもここのサイトを見ると身長なんかもGaussianに従うそうですよ!こんな感じで、Gauss分布っていろんなところに出没しているんです。
Gauss分布の特徴は??
なんか難しいなーと思っているそこのあなたに朗報です!このGauss分布って特徴付ける量が2つしかないんです。それはGauss分布の広がりと平均値です!
平均値はわかりやすいですね。上の図だと0が平均値ですし、IQであれば100、偏差値であれば50、身長であれば男性は170cm、女性は158cmとかでしょうか。つまりGauss分布の中心の値です。日本人の平均身長とオランダ人の平均身長の分布を取ったらその中心がずれるのは明らかなので、そこを記述する変数がGauss分布の平均値です。
そしてもう一つはその広がりです。例えばストップウォッチで10秒きっかりに時間を測定するという操作を10000回行う謎の実験を考えてみましょう(笑)私が寝起きでシャキッとしている時は割と10秒近辺でデータを取れると思いますが、一方でお酒を飲んでいい感じになっている時だと平気で5秒で止めたり逆に20秒くらいカウントすることも多いはずです(笑)そんな感じでデータの広がりの大きさがGaussianのもう一つの変数です。
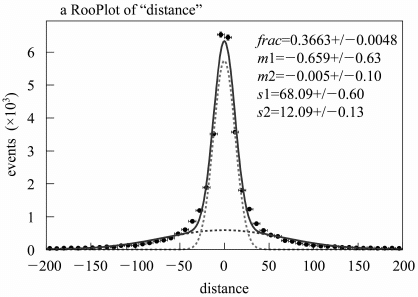
上の図だと縦にビシっとはいったGauss分布が寝起きの私、横に広がっただらしないGaussianがお酒を飲んでいる私だと思ってくださいw
ちなみにこの図はだらっとしたものとビシっとした2つの点線のGaussianを足し合わせて実線のような新たなGaussianをつくった「double Gaussian」というものです。これはシャープな活動銀河核の光とボワッとした母銀河の広がった光のプロファイルを足し合わせて、クエーサーのように明るくも裾野の広い天体の輝度プロファイルをモデル化する際などによく用いられています。
Gaussianは広がりが大事
さて、ボリンジャーに釣られてきた皆さま、お待たせいたしました(笑)この広がりこそがいわゆるsigmaなのです。ちょっとグラフを見てみましょう。
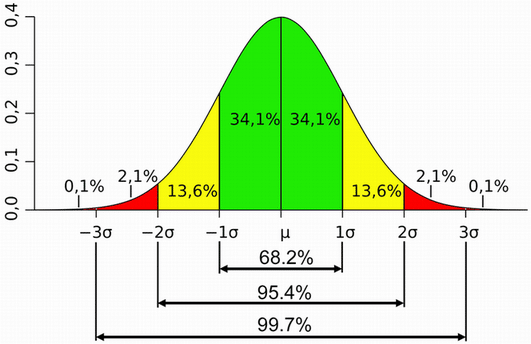
上の図だと緑の範囲が+/-1sigma、黄色が+/-2sigma、赤が+/-3sigmaです。sigmaっていうのがその分布の広がりを表しています。
一つだけ天下り式にいいます。このGaussianって全体で積分すると(つまり全体の面積を計算すると)その大きさが1になるんです。そして身長なり偏差値なりあなたの値があるわけですから、中心からあなたの値までを積分すると集団全体であなたがどの位置にいるのかが分かるわけです!(もしGauss分布とGauss積分に興味がおありであれば、「物理のための数学(和達三樹)、岩波書店」がオススメです!和達さんはマジでEinsteinに似ていますw)
例えばあなたの学校や会社で身体測定をし、男性の平均身長が170cm、その広がり(つまりsigma)が3cmだとしましょう。もしあなたが男性で身長が173cmであれば、あなたの身長はちょうど全体の1sigmaの位置です。そして上の図より1sigmaの面積は全体の68.2%ですので、身長が低い側も同じ程度に分布していると仮定するとあなたの身長は集団の中で68.2%に位置しています。そしてもしあなたの身長が179cmであれば、あなたの身長は集団全体で3sigmaの位置にあり、全体の99.7%とかなりレアなところに位置しています。このように計測した統計がGauss分布に従うのであれば、あなたが全体のどこに位置しているのかがわかります。
ボリンジャーとは??
ボリンジャーバンドはこのGauss分布を株価推移に当てはめたものです。そしてボリンジャーバンドの求め方はこのリンクにあります。
正直、私たち科学者が普段使っているGaussianや標準偏差からするとこの定義はかなり違和感があります。数学的にはこのボリンジャーの標準偏差は正しくないと言わざるを得ません。しかしながら、マクロな視点から株価変化を見ると「経験的に」正しいのだと思います。このパラグラフは読者の皆さんにとって意味がわからないかもしれませんが、科学者としての私の良心から書かざるを得ない文であることをご理解ください。
まあそんな難しいことは置いておいて、ボリンジャーバンドは考えている期間の中で想定しうるどの位置に今の株価がいるかってことです。でも今の株価は2sigmaだから95.4%の位置か・・・というのは意味不明なので、100-95.4=4.6%で今の株価を外れるのは4.6%...え、それってかなりレアじゃない!?くらいの解釈がちょうどいいと思います。そんな感じでボリンジャーバンドって統計学的には結構突っ込みどころもあるんですが、まあ今の株価の期待値やそこを外れるのはどの程度の確率か、くらいに捉えるといいと思います。
最後に
ボリンジャー、sigma、、、なんのこっちゃといった方にすこしでもそのエッセンスがお伝えできたら大変幸いです。
