
変分原理 2 - 架橋問題
前回の続き。橋が川に対して直角に架かることについて。
橋を直角に最短距離架けたい理由で一番ありそうなのはとってもお金がかかるから、という身も蓋もない理由です。防災や技術的要因もあるでしょうけれどそれらもお金があればかなりの部分解決できてしまうでしょう。
じゃあ一体、橋をかけるのにお金がどれぐらいかかるのか調べてみましょう。実際の橋の建設費を調べても良いのですが、それはあとにして計算だけで予想してみます。
橋のコストに応じて角度はどう変わるか計算してみよう
以下のように川の両側にある地点Aと地点Bをむすぶ道路を建設します。
橋の角度$${θ}$$は$${x}$$軸から反時計回りに測ります。$${θ=0}$$のときが川に対して直角ということです。

話を簡単にするためにAとBは対称の位置にあって橋(波線)はかならず原点を通ることにします。このとき陸路の長さはA側とB側で同じになります。
さらに道路の建設費を出すために$${橋のコスト係数:Pr,陸のコスト係数: P}$$を導入します。このとき道路の建設費は以下の通りになります。
ここからしばらく数式が続きます。読みたくない人は結論 - 橋のコストを変えていったときの最適角度だけ読んでください。
$$
建設費の合計 = 橋の建設費 + 陸路の建設費
$$
$$
橋の長さ = W / cos(θ)\\
橋の建設費 = Pr * 橋の長さ
$$
$$
陸路の長さ = \sqrt{(Ax - \frac W 2)^2 + (Ay - \frac W 2tan(θ))^2}\\陸路の建設費 = 2 * P * 陸路の長さ
$$
これで具体的な数値を与えて建設費が最小となる橋の角度を調べてみましょう。今後、地点の座標と川幅は以下の値で固定します。
$$
A(Ax,Ay) = (50, 50)\\川の幅: W = 20
$$
橋と陸とでコストが変わらない場合
$$
橋のコスト係数:Pr = 1\\陸のコスト係数: P=1
$$
橋の角度ごとに建設費を求めると以下の通りです。

計算結果は角度45度、最短距離の一直線が最適という結果になりました。これは当然ですね。
橋のコストが陸の3倍の場合
$${Pr=3}$$にして計算してみます。他の条件は変えません。
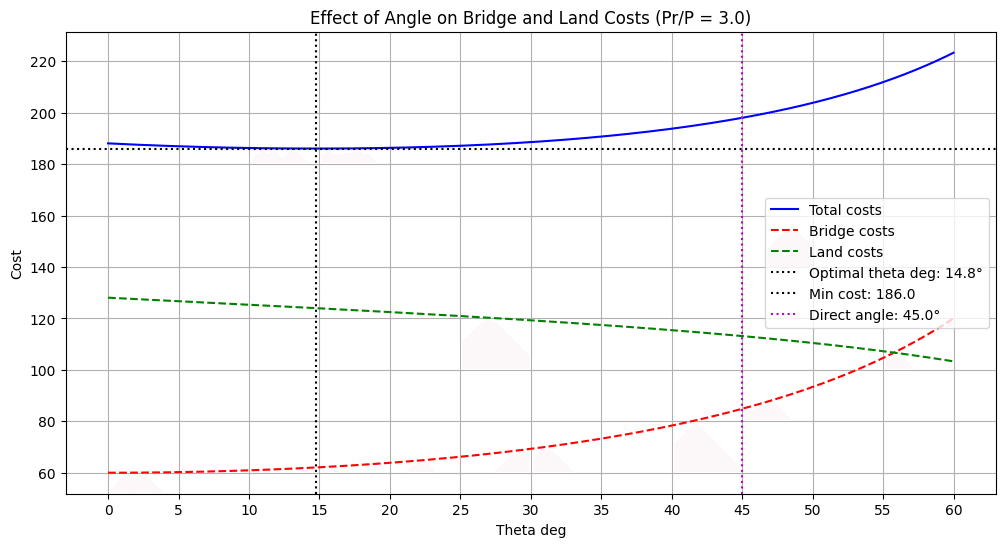
この場合、コスト最小角は15度になりました。一気に30度減りましたね。
結論 - 橋のコストを変えていったときの最適角度
同様に橋のコストを1~20倍にかえて費用最小となる角度を計算すると以下の通り。
皆さんは実際の橋のコストは陸の何倍ぐらいだと思いますか?
予想してみてください。

僕の予想は、橋を直角に架けることが常識化するには少なくともコスト10倍は必要に見えます。5倍程度までなら多少斜めにかけてもいいかなという気がします。
次回は実際の橋の建設費を調べてみましょう。
今回使ったプログラムの配布
地点の座標やコスト係数を自由に変えて計算とクラフの作成ができます。自由にご利用ください。生成AIで10分ぐらいで作ってもらいました。自力だとなんだかんだ1時間はかかったと思います。
いいなと思ったら応援しよう!

