
ユークリッドの互除法と不定方程式
はじめに
こんばんは.
ここでは,高校数学「数A」で扱われる,以下の2つの内容について説明していきます.
ユークリッドの互除法
・概要
・例
・一般化
・証明
ユークリッドの互除法の応用例:不定方程式
・概要
・例題
参考文献
note初心者ですので,ぜひ暖かい気持ちで見てもらえたら,と思います.
ユークリッドの互除法
1. 概要
ある2つの整数の「最大公約数」を求める計算方法です.
特徴として,最大公約数を「素因数分解よりも簡単に速く求められる」ことが挙げられます.
このときに用いられる重要な性質を以下に示します.
[重要な性質]
「割られる数と割る数の最大公約数」は,「割る数と余りの最大公約数」に等しい.
すなわち,割られる数(被除数)を$${a}$$,割る数(除数)$${b}$$,その商を$${q}$$,余りを$${r}$$とするとき,$${\mathrm{GCD}(a,b)=\mathrm{GCD}(b,r)}$$が成り立つ.
順番としては以下の通りです.
大きい方の整数を,小さい方の整数で割ったときの商と余りで表す
②その後「商を大きい方の整数」および「あまりを小さい方の整数」として,改めて商と余りを計算して表す
③①②を繰り返し,あまりが0となったときの「小さい方の整数」が最大公約数となる
2. 例
例として,「216」と「45」の最大公約数を,ユークリッドの互除法により求めてみます.
$$
216 = 45 \times 4 + 36\\
45 = 36 \times 1 + 9\\
36 = 9 \times 4 \quad \\
\therefore \mathrm{GCD}(216, 45) = 9\\
$$
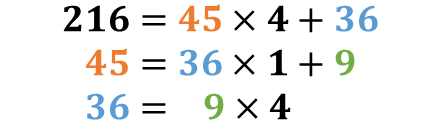
上記の式が(1)どのような性質をもとにしていて,(2)どういった計算をおこなっているのか,を以下に説明します.
[性質上の説明]
1行目:「216と45の最大公約数」=「45と36の最大公約数」
2行目:「45と36の最大公約数」=「36と9の最大公約数」
3行目:「36と9の最大公約数」= 9
この関係を等号で結んでいけば,「216と45の最大公約数」= 9が成り立つ.
[計算上の説明]
このとき,「余りの数」が「割る数(除数)」に,「割る数」が「割られる数」に,とズレていっているのが分かるでしょうか.
3行目の計算では,あまりが0となったため,計算終了となり,その時の割る数が「最大公約数」となります.
【注釈】
格好よく書くと,整数$${a,b}$$の最大公約数(Greatest Common Divisor)は,$${\mathrm{GCD}(a,b)}$$のように表されたりします.
通常は,日本語で「216と45の最大公約数は9である」と書いてもらって全然大丈夫です.
3. 一般化
ここで,この計算手順を文字式で表してみます.
任意の正整数を$${m, n (x > n)}$$とおく.
最初の計算式は,商$${q}$$と余り$${r}$$を用いて,以下のように表すことができる.(商:quotient,余り:remainder)
$$
m = nq+ r
$$
一般化するために,$${m = r_0, n = r_1}$$とおいてみる.すると,
$$
r_0 = q_0r_1 + r_2 \quad (0 < r_2 < r_1) \\
r_1 = q_1r_2 + r_3 \quad (0 < r_3 < r_2) \\
r_2 = q_2r_3 + r_4 \quad (0 < r_4 < r_3) \\
…
$$
と計算が続いていく.非負整数$${i}$$を用いて一般化すれば,
$$
r_i = q_i r_{i+1} + r_{+2}
$$
のように表せる.
このように計算を繰り返していき,$${i = h}$$回目で余りが0となったとき,すなわち
$$
r_{h-1} = q_{h-1}r_h + 0
$$
が得られたとき,求める解は$${r_h}$$であり,$${\mathrm{GCD}(r_0,r_1) = r_h}$$と表せる.
4.証明
ユークリッドの互除法が成立することを証明してみます.すなわち,
「2つの自然数$${a,b}$$について,$${a}$$を$${b}$$で割ったときの商を$${q}$$,余りを$${r}$$とするとき,『$${a}$$と$${b}$$の最大公約数』は,『$${b}$$と$${r}$$の最大公約数』に等しい」
ことを証明します.
[証明]
はじめに,条件より$${a = bq + r …(1)}$$
移項すれば,$${r = a - bq …(2)}$$
ここで,$${a}$$と$${b}$$の最大公約数を$${m}$$,$${b}$$と$${r}$$の最大公約数を$${n}$$とおく.
$${m}$$は$${a}$$と$${b}$$の最大公約数であるので,式(2)より$${m}$$は$${r}$$の約数であるといえる.(実際,$${a = ma', b = mb'}$$とおけば,$${r = ma' - mb'q = m(a'-b'q)}$$となるので,これが成り立つ.)
よって,$${m}$$は$${b}$$と$${r}$$の公約数であるといえる.
ここで,$${b}$$と$${r}$$の最大公約数は$${n}$$であるので,
$$
m \leq n …(3)
$$
次に,$${n}$$は$${b}$$と$${r}$$の最大公約数であるので,式(1)より$${n}$$は$${a}$$の約数であるといえる.(実際,$${b = na'', r = nr'}$$とおけば,$${a = na''q + nr' = n(a''q + r')}$$となるので,これが成り立つ.)
よって,$${n}$$は$${a}$$と$${b}$$の公約数だといえる.
ここで,$${a}$$と$${b}$$の最大公約数は$${m}$$であるので,
$$
n \leq m …(4)
$$
式(3)(4)より,これらを同時に満たすのは$${m = n}$$である.
したがって,「割られる数と割る数の最大公約数」は,「割る数と余りの最大公約数」に等しい.
[証明終]
不定方程式
1. 概要
まず,不定方程式とは何なのかを示します.
不定方程式:解の組み合わせが無数にあるような,整数係数による方程式
(これを一般化したものは「ディオファントス方程式」と呼ばれます)
ベズー方程式:ディオファントス方程式の中でも,$${ax + by = d}$$と表される方程式
センター試験では,「ベズー方程式を満たす整数$${x,y}$$の組み合わせを求める問題」が出題されます.そこで,これを解いてみます.
2. 例題
以下のような例題を考えます.
[問題]不定方程式$${8x+11y = 1 …(a)}$$について,以下の問に答えよ.
(a) 式$${(a)}$$を満たす整数の組み合わせ$${(x,y)}$$を1つ求めよ.
(b) 式$${(a)}$$を満たす整数の組み合わせをすべて求めよ.
[方針(a)]
不定方程式$${ax + by = r}$$(ただし,$${a,b}$$は互いに素)に対する,解法の順序を簡単に示します.
係数$${a, b}$$にユークリッドの互除法を適用し,関係式を導く
(余りが0となる式の1回分手前まで行う)各関係式を,余りについて解く(変形する)
余りが一番小さい式に,あまりが2番目に小さい式を代入する
3. で代入した式を整理する
(【重要】このとき,$${r = a \times b + c \times d}$$というように,「積の形」のまま残しておく)以降,3.と4.を繰り返し,$${r = a\times m + b\times n}$$という形に整理できたとき,組み合わせ$${(x,y)=(m,n)}$$が解となる
[解答(a)]
はじめに,11と8の最大公約数を求める.ユークリッドの互除法により,
$$
11 = 8 \times 1 + 3 \Leftrightarrow 3 = 11 - 8 \times 1 …(1) \\
8 = 3 \times 2 + 2 \Leftrightarrow 2 = 8 - 3 \times 2 …(2) \\
3 = 2 \times 1 + 1 \Leftrightarrow 1 = 3 - 2 \times 1 …(3) \\
$$
が成り立つ
次に,式(3)に式(2)を代入し,整理する(これを式(4)とする).
$$
1 = 3 - 2 \times 1 = 3 - {8 - 3 \times 2} \times 1 = 3 + 8 \times (-1) + 3 \times 2 = 3 \times 3 + 8 \times (-1) …(4)
$$
さらに,式(4)に式(1)を代入し,整理する(これを式(5)とする).
$$
1 = 3 \times 3 + 8 \times (-1) = (11 - 8 \times 1)\times 3 + 8 \times (-1) = 11 \times 3 - 8 \times 3 + 8 \times (-1) = 8 \times (-4) + 11 \times 3 …(5)
$$
式(5)と与式である式(a)の比較により,式(a)を満たす整数解の1つは$${(x,y) = (-4, 3)}$$
[解答(a) 終]
[方針(b)]
解は無限に存在しますが,これには規則性があり,整数$${k}$$を用いて一般化することができます.おおまかな解法を以下に示します.
不定方程式$${ax+by=r …(1)}$$(ただし,$${a,b}$$は互いに素)の解の1つが$${(x,y)=(m,n)}$$であるとする.
1. まず,式(1)に解を代入して式(2)とおく:$${am+bn=r…(2)}$$
2. このとき,式(1)から式(2)を引き,移項して式(3)とおく:$${a(x-m)=-b(y-n) …(3)}$$
3. ここで,a,bは互いに素であるので,$${x-m}$$はbの倍数であるといえる.これは,任意の整数$${k}$$を用いて$${x-m = bk …(4)}$$と表せる.
4. さらに,式(3)に式(4)を代入すれば,$${a\times bk = -b(y-n)}$$となるので,$${y-n = -ak…(5)}$$を得る.
5. これらより,一般解は
$$
x = bk + m, \quad y = -ak + n \quad (k \in \mathbb{Z})
$$
この流れに沿って,一般解を求めることができます.
[解答(b)]
設問の式(a)より,$${8x + 11y = 1 …(a)}$$
前問の式(5)より,$${8 \times (-4) + 11 \times 3 = 1 …(5)}$$
式(a)から式(5)を引いて移項すれば,$${8(x+4) = -11(y-3) …(6)}$$
ここで,8と11は互いに素であるので,$${x+4}$$は11の倍数であるといえる.これは,任意の整数$${k}$$を用いて$${x + 4 = 11k …(7)}$$と表すことができる.
さらに,式(6)に式(7)を代入すれば,$${8 \times 11k = -11(y-3) \Rightarrow y - 3 = -8k …(8)}$$が求まる.
ゆえに,一般解は
$$
x = 11k - 4, \quad y = -8k + 3 \quad (k \in \mathbb{Z})
$$
[解答(b) 終]
あとがき
いかがだったでしょうか.
今回重要であったのは,「ユークリッドの互除法という,シンプルに最大公約数を求める方法がある」こと,そして「不定方程式は,ユークリッドの互除法を用いると簡単に解けることがある」ということです.
不定方程式やユークリッドの互除法には,さらに深い話(定理や計算量,プログラムでの実装など)がありますので,興味のある方は調べてみてください.
何かわからないことや質問があれば,ぜひ気軽にどうぞ!
ここまでお読みいただき,ありがとうございました!
参考文献
ユークリッドの互除法 / Wikipedia
https://ja.wikipedia.org/wiki/%E3%83%A6%E3%83%BC%E3%82%AF%E3%83%AA%E3%83%83%E3%83%89%E3%81%AE%E4%BA%92%E9%99%A4%E6%B3%95ユークリッドの互除法の証明と不定方程式 / 高校数学の美しい物語
https://manabitimes.jp/math/672AtCoder版!マスター・オブ・整数 (素因数分解編) / Qiita
https://qiita.com/drken/items/a14e9af0ca2d857dad23
加筆
v1.1 / 2022-02-21
・章「不定方程式」において,式番号およびLaTeX記述のミスのほか,常体・敬体の表記統一不足となっている箇所を修正しました.
