株式ポートフォリオを評価するためのプログラムを作ってみました

はじめに

はじめまして。8gyuです。業務で大規模データを扱うこととなったためプログラミングを集中して学びたいと思い、AidemyのPremium Plan を始めました。せっかくなので習ったことを活かして今後も自分で使えるツールを作りたいと思い、大学時代に授業で習った分散投資を行う際のポートフォリオを評価するための手法をPythonで実装してみました。

本記事の概要

指定した複数銘柄をポートフォリオとして検討した際、リスク(収益に対する分散)が小さく、リターン(期待収益)が大きい投資比率を選定することを目標にプログラムを作りました。本来であればシャープレシオの計算も行うべきなのですが、今回は初めての試みなので割愛し有効フロンティアの可視化迄をスコープとします。

＊当方金融・プログラムともに駆け出しなもので、誤りや改善すべき点ございましたら是非アドバイスを頂けると幸いです。(したがってこのプログラムの結果を用いて投資された結果につきまして私は一切の責任を負いません。悪しからず><)

参考： 古川浩一・蜂谷豊彦・中里宗敬・今井潤一（2006).  基礎からのコーポレート・ファイナンス (リンク)

実装

まずは、必要なパッケージをimportし、3年分のデータが取得できるよう、end_dateに本日の日付, start_dateに3年前の日付を格納しました。

import pandas_datareader.data as web
import pandas as pd
import time
import datetime
from datetime import date,timedelta
import calendar
import math
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.style as style
style.use('fivethirtyeight')


#日付取得
end_date = datetime.date.today()
start_date= end_date + timedelta(weeks=-52*3)

次に、各銘柄の終値を取得する関数を作成し、指定した銘柄についてstart_date からend_dateまでの各日の終値を取得しました。今回はweb.DataReaderメソッドを用いてyahooファイナンスからデータを取得しました。今回は今をときめくGAFAMを対象としました。

#各株銘柄取得 & 終値を取得
def get_Adj_Close(company):
   data = pd.DataFrame(web.DataReader(company,'yahoo',start_date, end_date))
   Adj_Close = data['Adj Close']
   return Adj_Close
   
CompanyList =　['GOOGL','AMZN', 'FB','AAPL', 'MSFT']

DF=pd.DataFrame()
for i in CompanyList:
   DF = pd.concat([DF, get_Adj_Close(i)],axis=1)
DF.columns = CompanyList

#時系列分析を行うため、indexをdatetimeに
DF.index = pd.to_datetime(DF.index)

#週次で集約
DF_W=pd.DataFrame(DF.resample('W').last())

#可視化
DF_W.plot(figsize=(7, 7), linewidth = 1)
sxmin='2018-02-15'
sxmax='2021-02-27'
xmin = datetime.datetime.strptime(sxmin, '%Y-%m-%d')
xmax = datetime.datetime.strptime(sxmax, '%Y-%m-%d')
plt.xlim([xmin,xmax])

amazon, Google の株価の上がり方が凄く大きく見えますね。

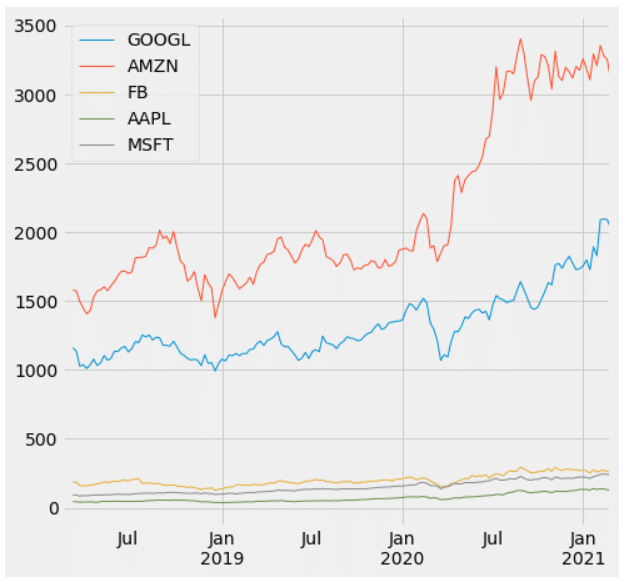
ただ、オーダーが違うので変化が見えないだけで、軸を変えれば他3株も大きく動いています(以下Appleです。)

次に4か月ごとのリターン(期待収益率)とリターン(収益率の標準偏差)を求めました。収益率につきまして、今回は対数収益率 = log e (今回株価 / 前回株価)　を用いました。

通常思い浮かべられる変化率(今回株価 - 前回株価) / 前回株価　を用いると、株価の上昇と下降が同じだけ起こった場合に増分の比率を大きく表してしまうという懸念点があります。対数収益率を用いることで増分、減少分を等価で計算することができます。それぞれ、4か月分の値を求めました。

#対数収益率を求め, 4か月ごとの期待収益率と期待標準偏差を求める
DF_W_log=np.log(DF_W).dropna()
DF_W_logdiff= DF_W_log.diff()
DF_W_logdiff_mean=DF_W_logdiff.mean(axis=0)
DF_W_logdiff_mean_4months=DF_W_logdiff_mean*15
DF_W_logdiff_stdv=DF_W_logdiff.std(axis=0)
DF_W_logdiff_stdv_4months = DF_W_logdiff_stdv * math.sqrt(15)

さて、上記の計算により個別株のリスクとリターンを計算することができたのですが、今度は複数株を組み合わせたポートフォリオとしてのリスク・リターンを求めたいと思います。

ポートフォリオとしてのリターンは割と想像しやすいと思います。各株の比率を wi , リターンをμi で表すと、ポートフォリオのリターンμpは

μp =  wa × μa + wb × μb + ....+ wn × μn(個別株の加重平均)で求まります。

一方、ポートフォリオとしてのリスクは個別株の持つリスクに加え、一方の株が上がったときにもう片方の株が下がる(上がる) といった共分散の大きさと個別株の持つリスクの掛け合わせを総当たりで計算し加重平均したものとなります。個別株のリスクをσi 、共分散をCov(i,j) とし数式で表すと、

ポートフォリオのリスクσ^2 p 

= wa^2 ×σa^2 + ... + wn^2 ×σn^2 :  (個別株の持つリスク) 

+ wa × wb × Cov(a,b) + wa × wc × Cov(a,c) + .... + wn × wn-1 × Cov(n, n-1) : (総当たりですべての組み合わせについてのリスク) 

で求まります。平方根を取ることで、個別株のリスクと並べることができます。

上記の考え方を実装しました。

まず、相関係数/共分散行列を作成しました。相関係数については、pythonのメソッドcorr()が便利で、一発で計算をすることができました。

共分散については、上記で求めた相関係数と収益率の標準偏差を用い、

Cov AB (株式A,Bの共分散) = ρAB (株式A,Bの相関係数) × σ(収益率の標準偏差: 株式A) × σ(収益率の標準偏差: 株式B) の式で求めました。

#相関係数行列/共分散行列作成
cor_DF = DF_W_logdiff.corr()
multi_stdv=np.zeros((len(DF_W.columns),len(DF_W.columns)))
for i in range(len(DF_W.columns)):
   for j in range(len(DF_W.columns)):
       multi_stdv[i,j] = DF_W_logdiff_stdv_4months[i] * DF_W_logdiff_stdv_4months[j]
cov_DF = multi_stdv*np.array(cor_DF)
pd.DataFrame(cov_DF)

求まった共分散が上記です。

これですべての計算ピースは求まったことになります。あとはポートフォリオを計算するだけなのですが、最適な組み合わせは、どうやって求めればいいのでしょうか。

ここでモンテカルロ法と呼ばれる手法を用います。乱数を多数発生させることにより、疑似的に組み合わせを作り、各組合せのリスクとリターンを計算するのです。乱数を1セットにつき株式の数だけ発生させ、それぞれの数 / 合計値を求めることで比率を作りました。今回は50000通りの組み合わせを作成してみました。

#指定した回数乱数を発生させる関数
def simulate(num, df):
   b=[]
   for i in range(num):
       a = []
       for j in df.columns:
           rand = np.random.rand()
           a.append(rand)
       b.append(a)
   return pd.DataFrame(b, columns = df.columns)
   
#確率行列を作るための関数
def prob_simulate(df):
   b=[]
   for j in range(len(df)):
       a = []
       for i in range(len(df.columns)):
           prob = df.iloc[j,i] / sum(df.iloc[j,:])
           a.append(prob)
       b.append(a)
   return pd.DataFrame(b,columns = df.columns)

#第一引数は試行回数今回は50000通り
sim = simulate(50000, DF_W)
   
#確率行列
prob_sim = prob_simulate(sim)
Output = prob_sim      
   

仕上げです。上述のポートフォリオのリスク、リターンを求めるプログラムを作成し、上で作った組み合わせごとのリスク、リターンを計算しました。

#分散, 標準偏差を計算
def Portfolio(df,cov,exp):
   a = []
   b = []
   c = []
   for i in range(len(df)):
       prob_dual = np.zeros((len(df.columns),len(df.columns)))
       for j in range(len(df.columns)):
           for k in range(len(df.columns)):
               prob_dual[j,k] = df.iloc[i,j] * df.iloc[i,k]
       a.append(sum(np.diag(cov * prob_dual)))
       b.append(np.dot(np.array(df)[i], np.array(exp)))
   c = np.sqrt(a)
   d = pd.DataFrame(a,columns=['Portfolio_cov'])
   f = pd.DataFrame(b,columns=['Return'])
   e = pd.DataFrame(c,columns=['Risk'])
   return pd.concat([df,d,e,f],axis=1)
   
plt.scatter(Result['Portfolio_stdv'], Result['Portfolio_exp'], s=1)
plt.title("Portfolio")
plt.xlabel("Risk")
plt.ylabel("Return")
plt.show()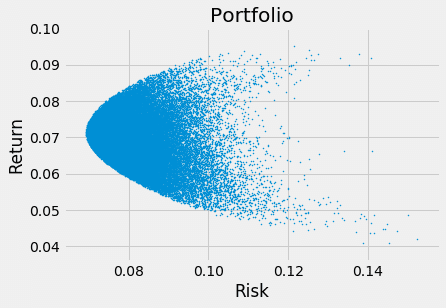

でました！！これが求めたかったポートフォリオのリスク、リターンです。一つひとつの点が(Google: 20%, Apple 30%, Facebook 10%, Amazon 10%, Microsoft 30%) のような比率を持った際にリスク、リターンがどこに位置するかを表しています。

例えば下のようなポートフォリオを選ぶのなら... 

同じリスクでよりリターンの見込める下の投資比率を選んだ方がより賢い選択と言えそうです。

リターンを最大にするようなポートフォリオの集合のことを有効フロンティアと呼びます。

せっかくなので、少し組み合わせを見て終わります。ご拝読感謝いたします。

#  0.001桁まで落として、ユニークな物からリスクの低い/リターンの高いものを選抜
from decimal import Decimal, ROUND_HALF_UP
Result['Risk_R'] = Result['Risk'].map(lambda x: float(Decimal(str(x)).quantize(Decimal('0.001'), rounding=ROUND_HALF_UP)))
Result_sort = Result.sort_values('Return',ascending = False).sort_values('Risk_R', ascending = True)
# 
Result_Opt = Result_sort[Result_sort['Risk_R'] < Result_sort['Risk_R'].unique()[3]]
Result_Opt = Result_Opt.reset_index(drop=True)
Result_Opt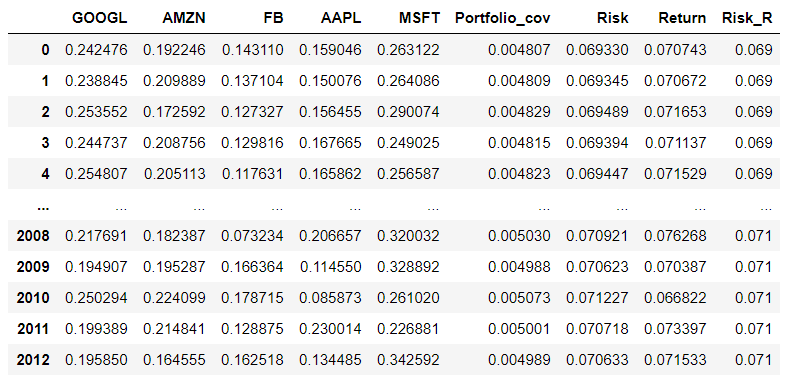

まとめ

無論、機械学習についてもAidemyコースの中でたくさん学びましたが、私にとって一番関心の高いものを題材にしてみました。次の機会に機械学習を用いた分析もやってみたいと思います。コースでならったデータ処理の方法(関数, numpy, Pandas, 可視化, web からの情報取得, 配列計算 等)を最大限駆使して、役に立つものを作れたことで少しだけ自信が付きました。