
【Tableau】CORR関数を活用して相関マトリックスを作成し散布図と連動させてみた。
こんばんは、Data Saber - Bridge 3rdに挑戦中のeightmanです。90日あった期間も残り僅かとなってきました。ギリギリのところを攻めていますが最後まで諦めずに頑張りたいと思います。
さて、今回は、前回の投稿でご紹介した、「縦持ち自己結合による散布図」から発展し、その散布図の相関係数を相関マトリックスで表現してみたいと思います。
※前回の投稿内容はこちらからどうぞ
1.本投稿のきっかけ
前回の投稿で複数の項目を自由に選択して散布図を表現する方法をご紹介しましたが、実際にその項目間にどの程度相関があるかを数値で把握するには相関係数を確認する必要があります。
散布図の傾向線にカーソルを合わせると、以下の通り「R-2乗」が表記されます。
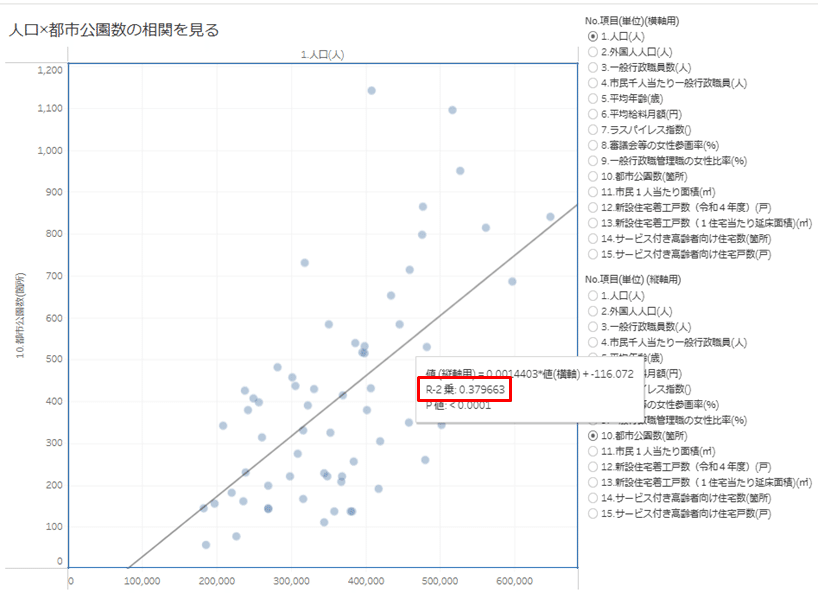
「R-2乗」とは「決定係数」のことであり、「相関係数」の2乗の値を指します。2つの数値の関係は以下の通りです。
0≦決定係数≦1
-1≦相関係数≦1
決定係数=(相関係数)²
決定係数=<|相関係数|ここでは、両係数の詳しい説明は割愛しますが、以下の記事がわかりやすかったので参考に掲載させていただきます。
【参考】決定係数について【相関係数と同じようで違うのです】】
https://sigma-eye.com/2018/10/22/the-coefficient-of-determination/
決定係数=(相関係数)²ということは、つまり相関係数を算出するには√R-2乗を計算する必要があります。
Tableau Desktop上であれば傾向線にカーソルを合わせて、右クリック→「傾向モデルの説明」をクリックで以下の通り「傾向モデルの説明」という表記がされますが、肝心な相関係数の表記はありません。
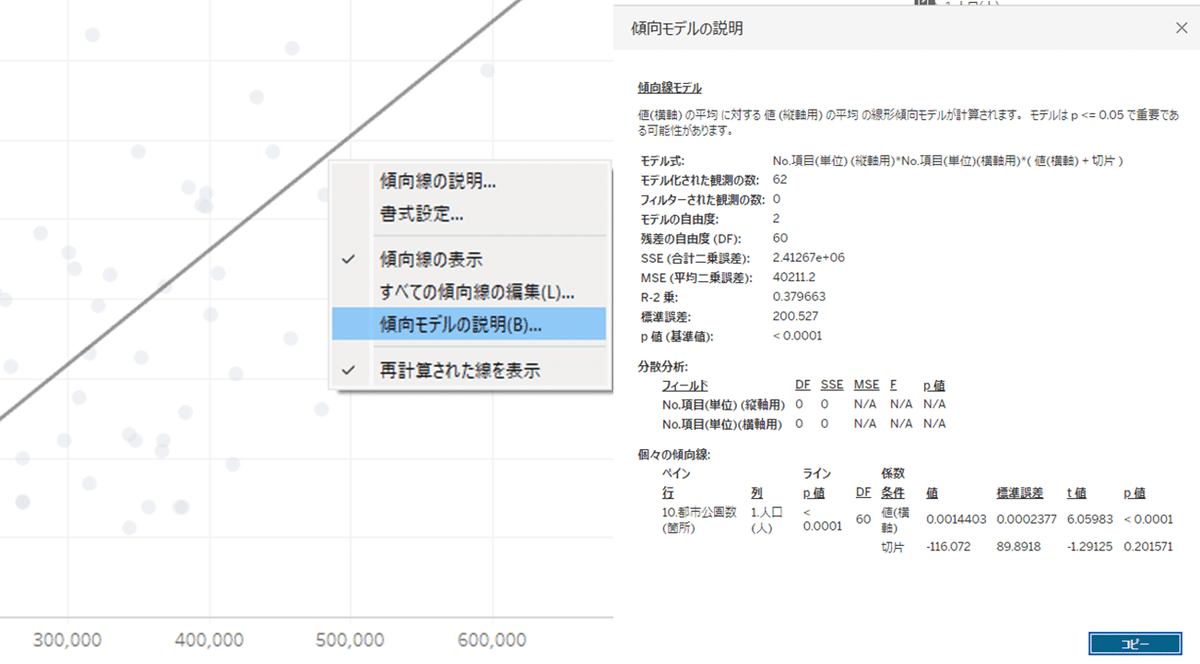
「相関係数はおよそ~です」とは言えないですよね。
また、統計データ等の多くの項目間の相関を把握したい時に、一回一回散布図を作成して傾向線で確認するのはかなりの手間となります。
そこで、一度に各項目間の相関係数をマトリックス表記し、係数と散布図が連動する仕組みを作れないかと考えました。

2.相関係数の出し方【CORR関数を活用】
今回は、ピアソン相関という、2 つの変数 x と y が正規分布しているとみなせるとき、それらの間にどの程度の相関があるかを調べる方法を使って相関係数を算出します。
ピアソン相関については、以下を参考にしてみてください。
【参考】
実際の計算式は以下の通りです。ん~数式だけ見ると難解ですね。

これをTableauでは以下の通り一つの関数で算出することができます。ちなみにExcelのデータ分析ツールでも可能です。
ピアソン相関係数=CORR(メジャー1,メジャー2)3.相関マトリックスを作成する。
CORR関数を使って、前回の散布図データで相関係数を算出し、マトリックス表を作成します。
まずは、以下の通りディメンションを列シェルフ、行シェルフに入れます。
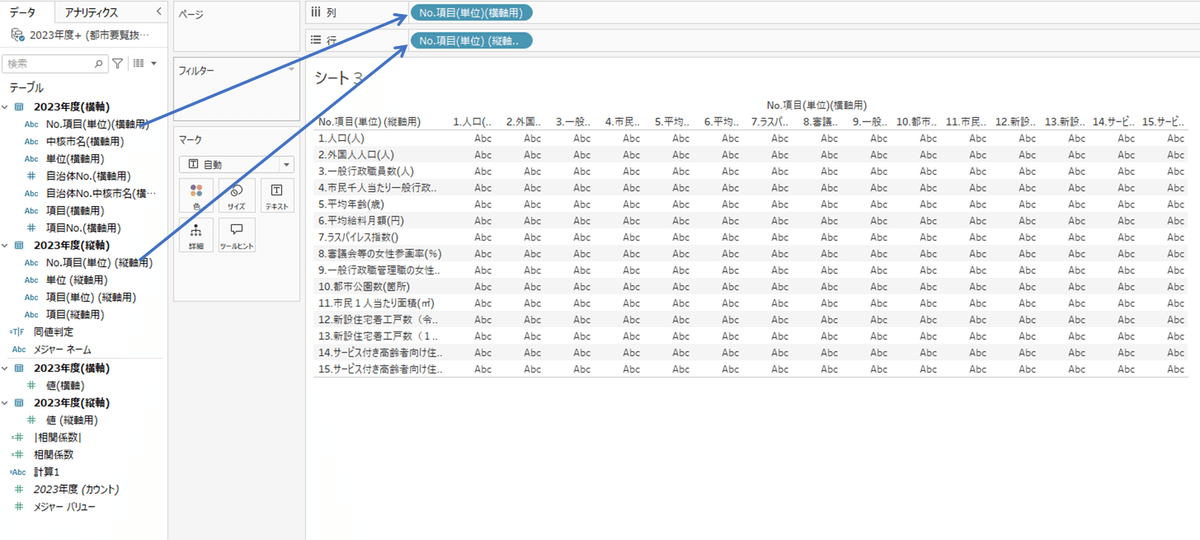

CORR([値(横軸)],[値 (縦軸用)])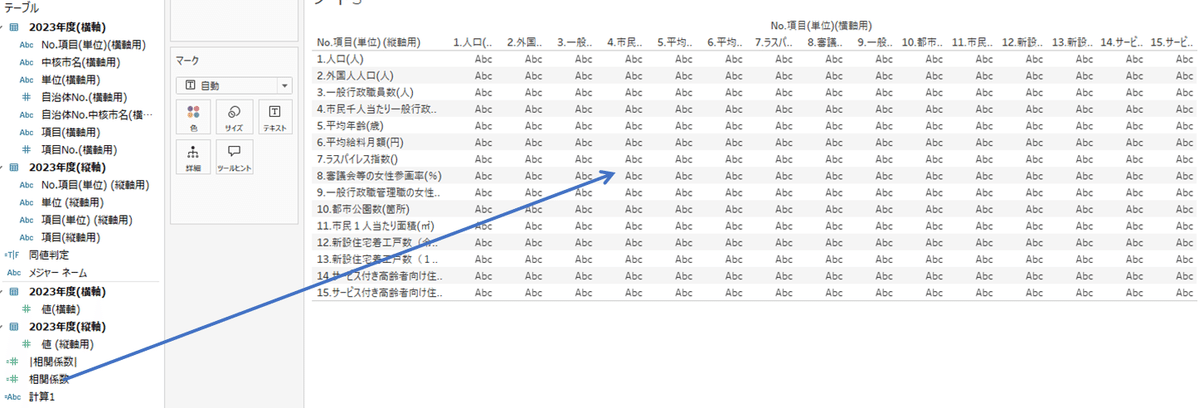
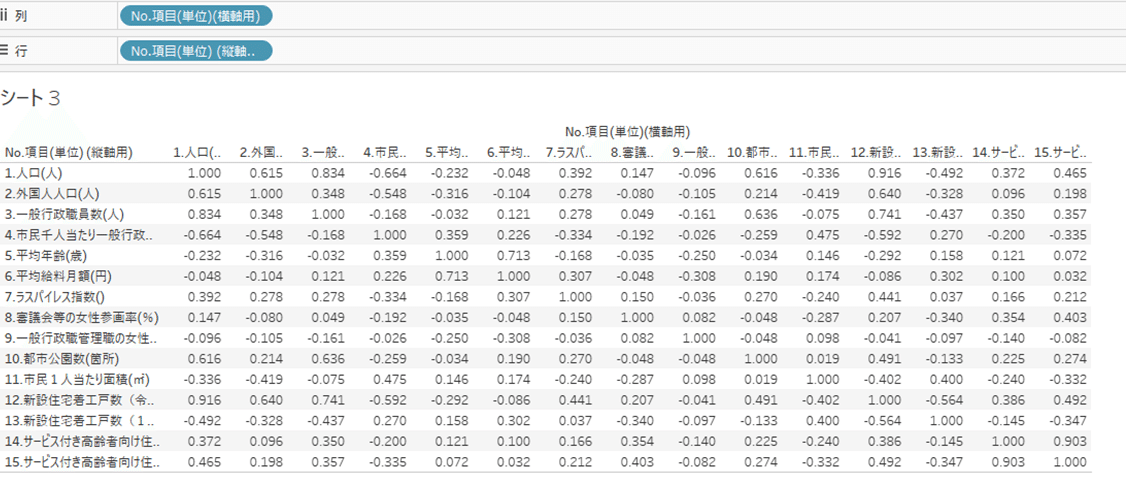
ただし、同じ項目同士の相関係数=1が含まれているので、フィルターを使って表記させないようにします。
同値判定という計算式を作成し、フィルターシェルフに入れ、「真」のみにチェックをいれます。

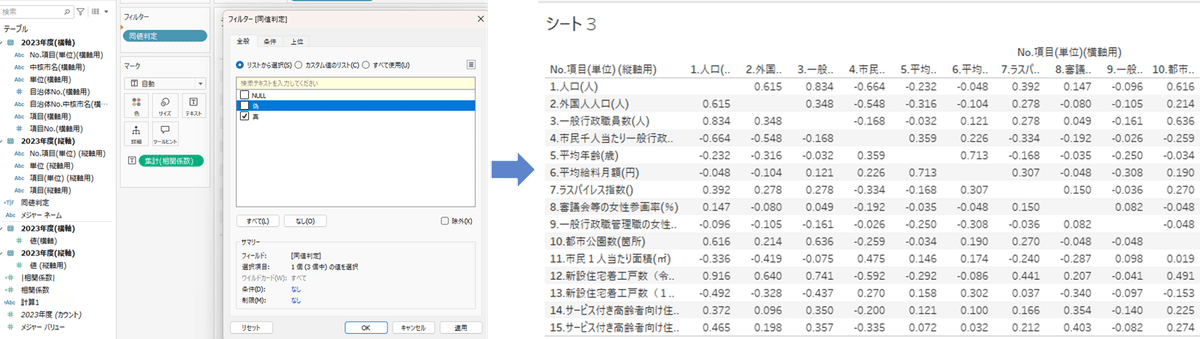
ここまでくれば、ほぼ完成す。以下はお好みでどうぞ。
①|相関係数|(絶対値)をABS関数で作成し、フィルターシェルフに入れて、表記したい相関係数の閾値(最小値)を設定する。
②ヒートマップ表現にするため「相関係数」メジャーを「色」に、表記方法を「四角」にする。
③行、列のフィールドラベルを非表示にする。
④ツールヒントの中身を整理する。
⑤ビュー表示を「標準」→「ビュー全体」にする。

今回は自己結合データで作成したので、対角線を境に同じ相関係数が表記されています。
4.ダッシュボード上で相関係数を散布図と連動させてみる
前回の投稿で作成していた散布図と今回の相関マトリックスを組み合わせてみます。
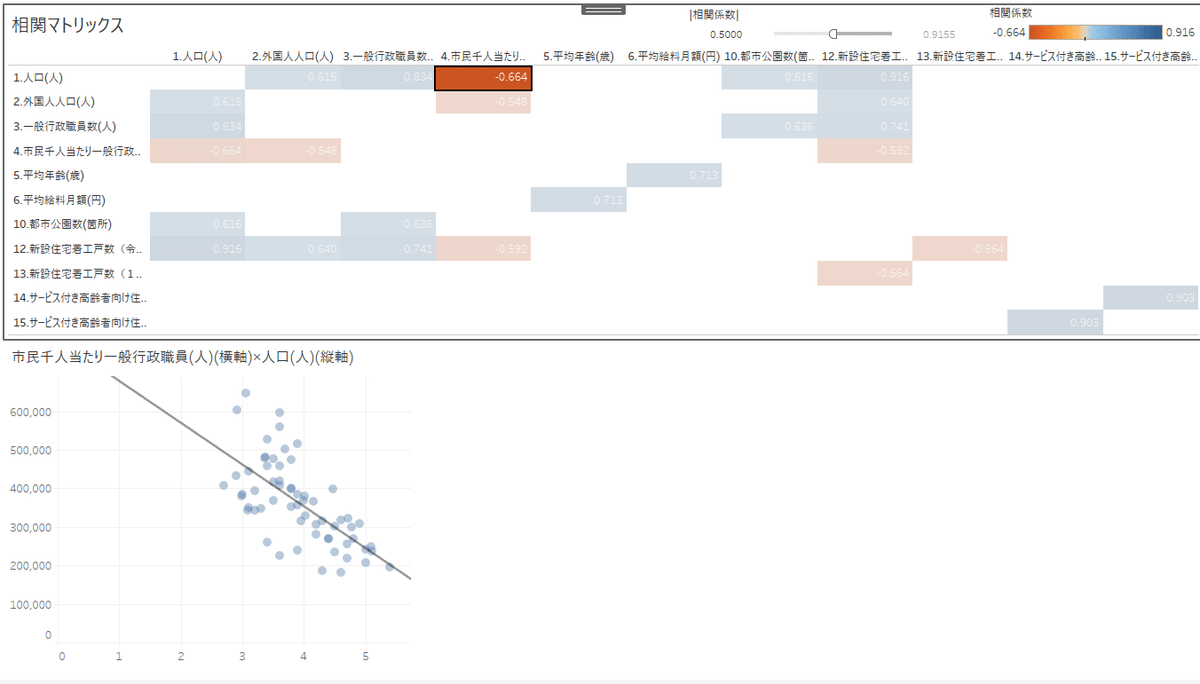
2つのグラフをダッシュボード上に配置し、ダッシュボードアクションを以下の通り設定します。

散布図のワークシートで、列・行シェルフに配置していたディメンションを取り除きます。
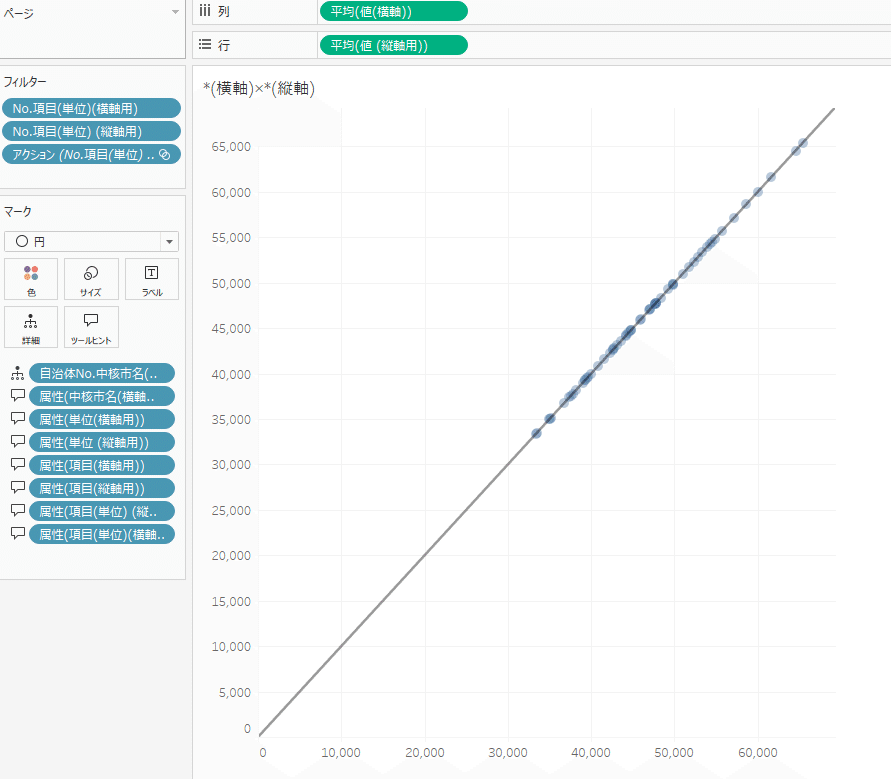
このままだと、各項目や単位がわかりにくくなってしまうので、タイトルの表示方法を変えることで対応します。

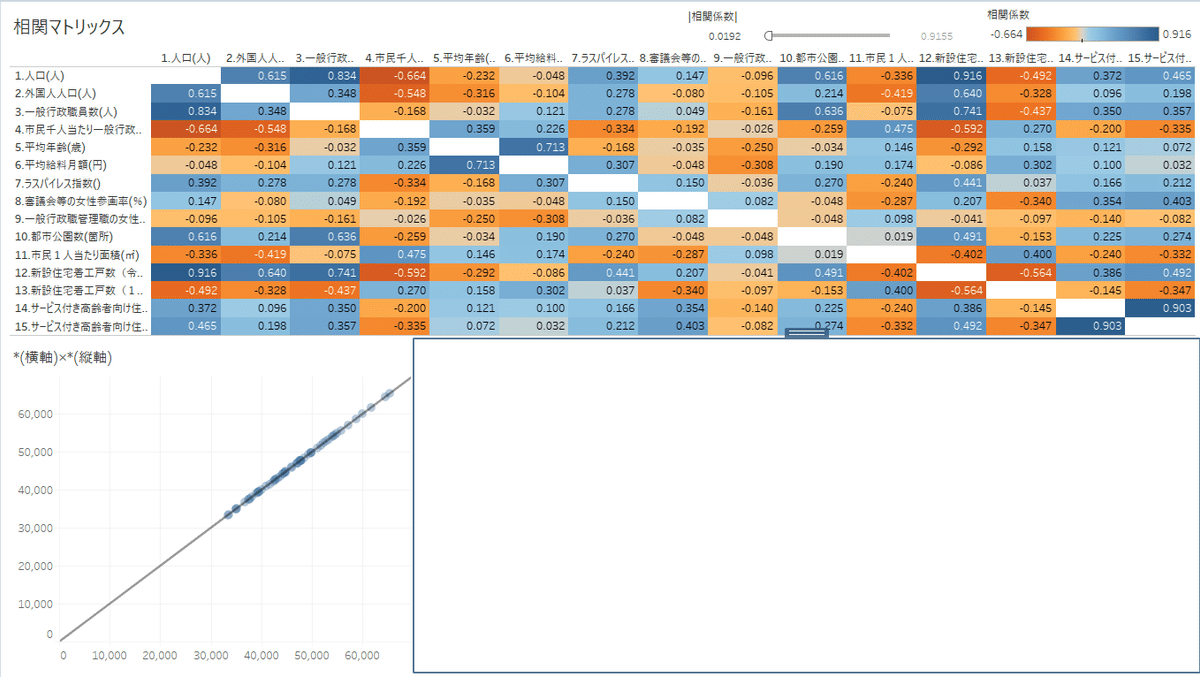
相関係数の凡例や、|相関係数|フィルターの配置を浮動にしてバランスよく配置して完成です。右下が空白で不格好ですが、今回はここで終了です。
5.おわりに
今回は、分析が目的ではないので各項目間の相関係数を見て深堀りしていくことはしないのですが、今回のような統計データを扱う際は「人口1人当たり~」、「行政職員1人当たり~」、「面積1平方キロメートル当たり~」等の数値を用意することで、自治体の規模にとらわれずに比較することができるようになりますね。
今回少し面白いなと感じたのは、「人口」と「一般行政職員数」は相関係数0.8と強い正の相関を持っており、対する「人口」と「市民千人当たり一般行政職員数」の相関係数は-0.6と比較的強い負の相関を持っていることが読み取れました。
人口が多いほど、公務員1人が受け持つ市民が多い(負担が大きい)ことがわかります。例えば、松山市は人口19万人で市民千人当たりの職員数が5.4人、船橋市は人口60万人で市民千人当たりの職員数が3人です。
もちろん正規職員の代わりに非正規職員が対応している可能性等もありますが、こういったことが一目でダッシュボード上で確認できるのは、やはり良いですし、意見交換が活発になりそうです。
今回の内容は汎用的に利用できると思いますので、様々な統計データ等を使って試していきたいと思います。
最後までご覧いただきありがとうございました。
今回のダッシュボードは以下に掲載しています。
