
確率・統計と受験数学~入試問題を楽しもう❣
大学入試、受験数学、数Ⅲ、高校数学、微積分学基本定理、合成関数の微分、分布関数、密度関数、確率変数、標準正規分布、カイ自乗分布
👉はじめに
難易度⭐⭐⭐
今回の記事は
●高校で数Ⅲをかじったことがある方
●受験数学に関係する方(学校や塾・予備校の先生、受験生、保護者…)
●確率・統計に興味がある方
を対象に書きました❣
入試問題のネタって自分の専門分野に近いところから探しがちだと思うんです。私の場合、確率や統計のネタから高校の範囲で扱えるものを選ぶことが多かったかな。計算問題にしても、意味のないメンドクサイ問題を出すのは心苦しいので、背後に数学的な意味のある何かが隠れているものを選びたくなってしまうんですね。
勿論、受験数学マスターのような先生がパズル的な問題を出題されることもあるので一概には言い切れませんが、入試問題は大学や出題者の豊かな個性を感じ取れて、改めて面白いな~と思います❣
毎年どこかの大学で「問題の傾向が変わった!」という情報が飛んでザワつきますが、出題者が変われば傾向は変わります。入試問題は複数の生身の人間が作り、メンバーはいつか必ず入れ替わりますもん。傾向対策は大切ですが、あっさり裏切られることはよくあるので予備校や塾を攻めないで(笑)。
一方、数学の基本は決して変わることなく裏切りません。…やはり大切なのは基本!
前置きが長くなりましたが、今日はこういった雰囲気をちょっと味わってもらおうと、高校数Ⅲの範囲の計算問題を紹介して、背後にある確率・統計の分野の背景をサクッとお話しします😊
では問題です。
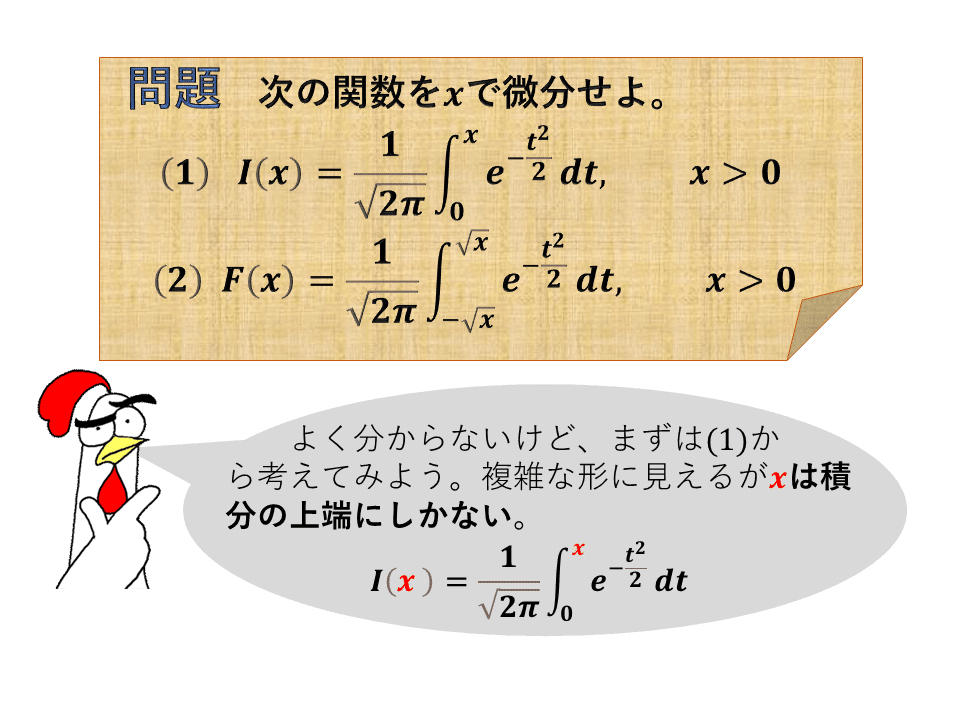
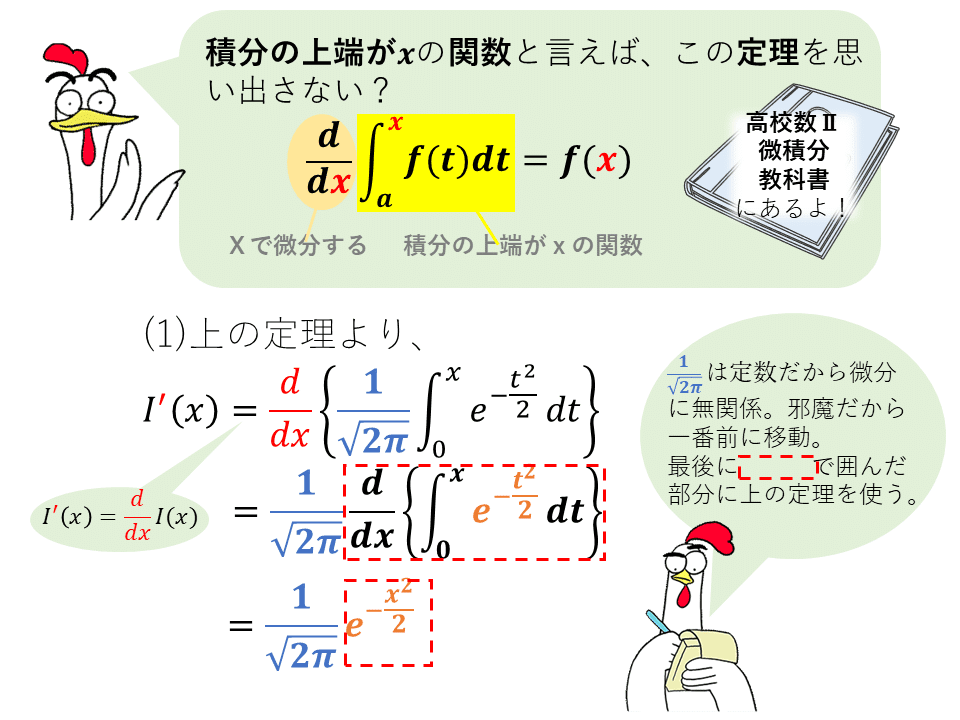
(1)の答は出たので次は(2)です。
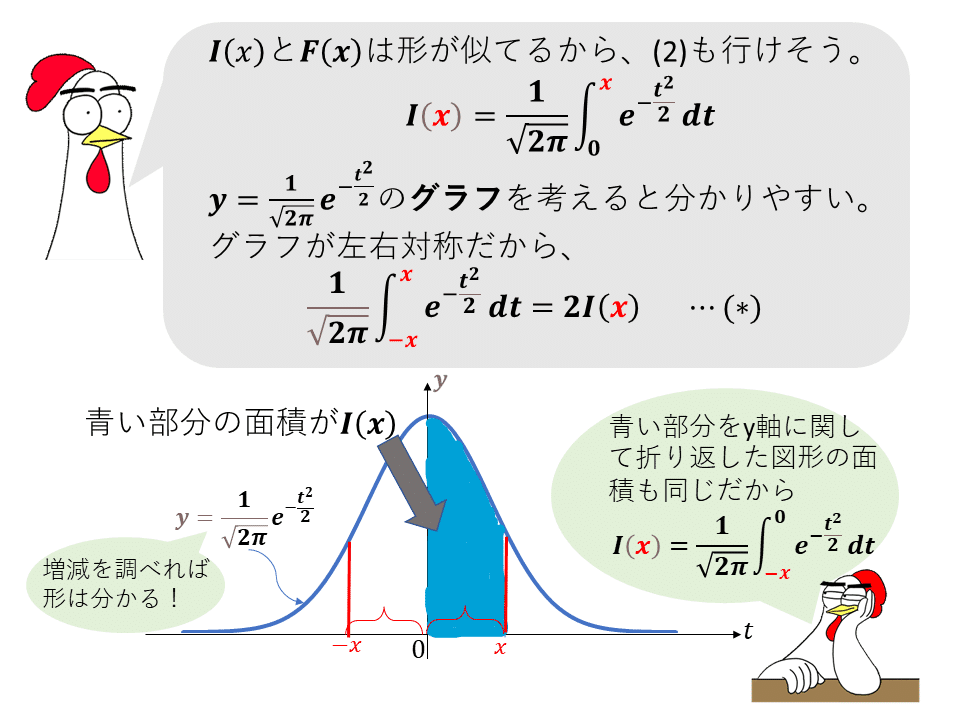
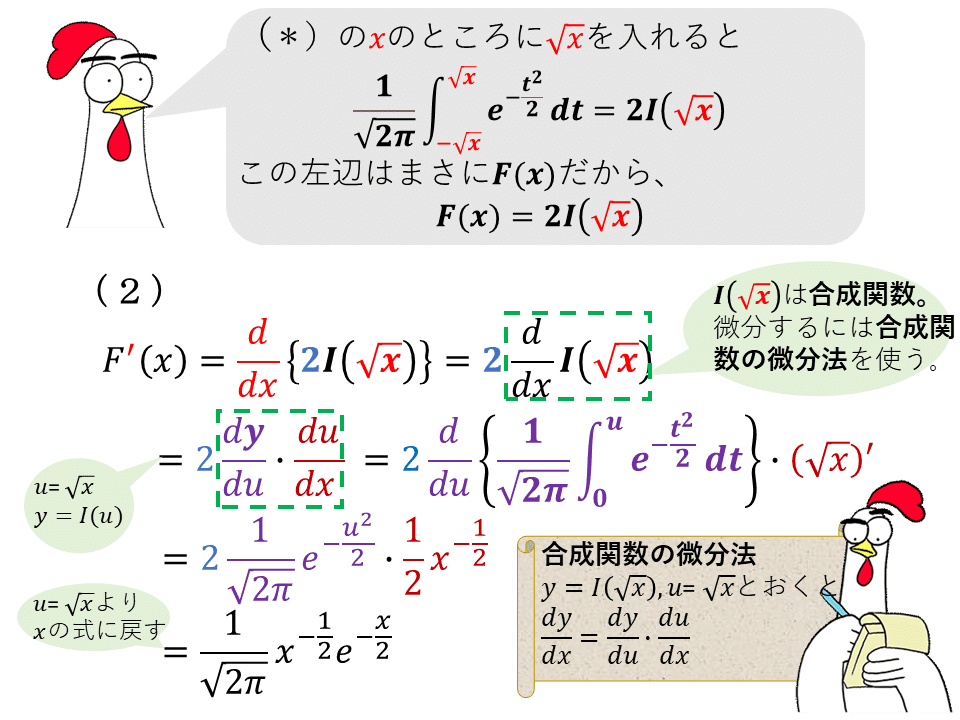
答えが出揃ったので、背景のお話です。
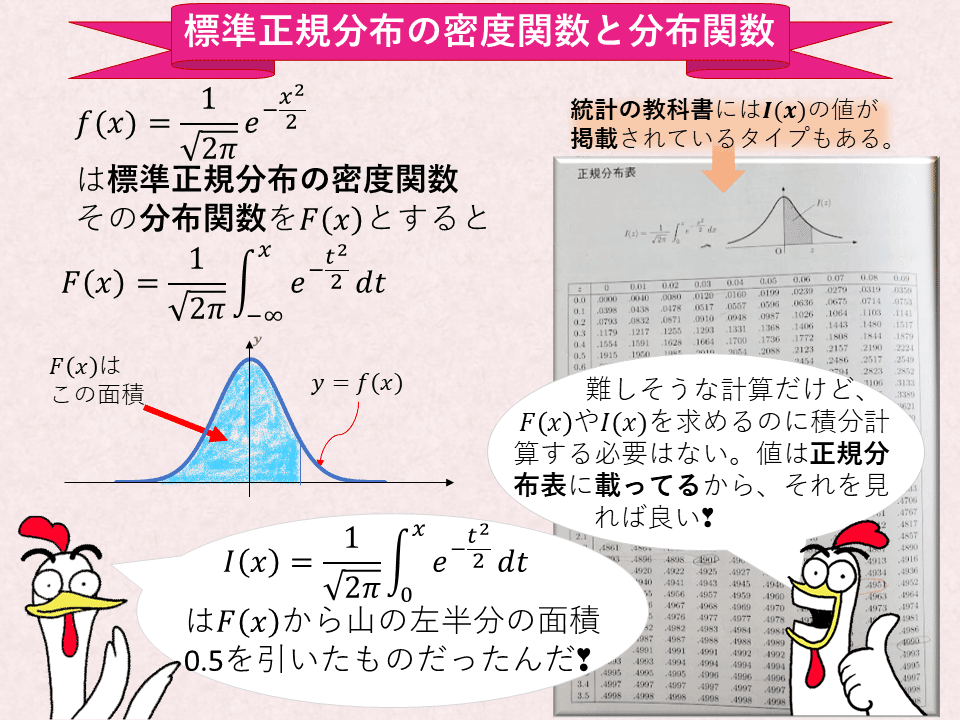
(1)の答は標準正規分布の密度関数になってることにお気付きでしょうか?
そして(2)の関数F(x)は関数I(x)と√xの合成関数になっていることが分かります。実はこのF(x)は、統計学で凄く重要なカイ二乗分布という確率分布の分布関数なのです。従って(2)の答はその密度関数となります。
この辺の話をイラスト解説でどうぞ❣

㊟”エックスの2乗分布"みたいに見えるが“カイ二乗分布”と読む。
今回は、無味乾燥に見える計算問題にも確率・統計の重要なトピックスが隠されていることはよくありますよ~というお話でした。受験生もそうでない方々も「何が隠されているのかな?」という視点で入試問題を楽しむのもアリですよ♪
ではまた~👋
