ギャンブラーの誤謬ではない⁉ ラルフ・ビンスの実験結果に異議あり!!

ギャンブラーの誤謬

例えば、コイントスを5回行います。

その結果、5回連続して表が出たとします(可能性としてはあり得ます)。

続いて、6回目のコイントスを行うのですが、ある人はこう考えます。

ここまで５回連続して表が出たのだから今度は裏が出るんじゃないか。

このように考えてしまう状態をギャンブラーの誤謬と言います。

なぜ、ギャンブラーの誤謬を取り上げたかというと、先日読んだ下記の本に興味深い内容が紹介されていたからです。

• 『87歳、現役トレーダー シゲルさんの教え 資産18億円を築いた「投資術」』 藤本 茂(著)

私が興味を持ったのは、ラルフ・ビンスの実験というものです。

「ラルフ・ビンスの実験」というものがあります。プログラマーのラルフ・ビンスは、博士号を持つ40人にゲームをしてもらいました。そのゲームのルールは次のとおりです。
①抽選箱の中には当たりが6本、ハズレが4本入っている
②当たりが出れば掛け金は2倍、ハズレが出たら掛け金は没収
③元手1000ドルで、1回に掛ける金額は自由
④ゲームを100回繰り返す
(中略)
40人の参加者のうち、資産を増やしたのは2人しかいませんでした。博士号を持っている「賢い」人間でも、95%は負けてしまったのです。
負けた95%は、「負けたあとに掛け金を増やし、買ったあとには減らす」という賭け方をしていました。

『87歳、現役トレーダー シゲルさんの教え 資産18億円を築いた「投資術」』
「コラム④ 多くの投資家は退場していく」より

ポイントは、下記の一文です。

• 負けた95%は、「負けたあとに掛け金を増やし、買ったあとには減らす」という賭け方をしていました

つまり、私の理解は以下の通りです。

• ハズレが出たのなら、次はアタリが出るだろうと予想して掛け金を増やした

• アタリが出たのなら、次はハズレが出るだろうと予想して掛け金を減らした

しかし、ラルフ・ビンスの実験では、当たりが出るかハズレが出るかは、完全に発生確率に依存しており、前回の結果による影響を受けません。

このため、負けた人は、ギャンブラーの誤謬にハマってしまったと考えられているようです。

ラルフ・ビンスの実験結果に異議あり!!

しかし、私は、負けた人の行動は正しかったと考えます。

その根拠は、以前読んだ下記の本に紹介されていた大数(たいすう)の法則とマーチンゲール法(別名: 倍賭け法)です。

• 『はじめての統計学 レジの行列が早く進むのは、どっち!?』 サトウマイ著

大数の法則とは、試行回数が増えるにつれて、その確率に収束していくというものです。

ラルフ・ビンスの実験では、ゲームを100回繰り返すというのが試行回数となります。

また、マーチンゲール法とは、勝率が50％, 配当が2倍であるギャンブルの必勝法で、賭けに負けた場合は賭け金を負けた金額の2倍にして勝つまでやるというものです。

ラルフ・ビンスの実験では、負けた95%の人が行っていた、負けた後に掛け金を増やし、買ったあとには減らすというのがマーチンゲール法です。

しかも、ラルフ・ビンスの実験は、勝率が60%ですから、マーチンゲール法で負けるはずがないのでは? というのが私の理解です。

ただし、気になる点が2つあります。

1. ゲームの試行回数が少なく大数の法則が成り立たないのかも

2. 元手が少なくマーチンゲール法を実行できないのかも

それにしても、95%の人が負けるという結果は信じられません。
(? _ ?)ﾎﾝﾄ?

そこで、ラルフ・ビンスの実験を検証してみることにしました。

ラルフ・ビンスの実験をPythonプログラムで検証してみた

ラルフ・ビンスの実験をPythonプログラムで検証してみました。

Pythonプログラムのソースコードは、下記となります。

import numpy as np
import matplotlib.pyplot as plt


def main():
    # くじ引きの用意
    ElementList = ['0', '1'] # 0: ハズレ、1: アタリ
    ProbList = [0.40, 0.60] # ハズレ40%, アタリ60%
    SampleSize = 100 # 試行回数
    People = 40 # 参加者

    Results = []


    # ラルフ・ビンスの実験 メインルーチン
    for p in range(People):
        print('第', p, '人目')

        Samples = np.random.choice(a = ElementList, size = SampleSize, p = ProbList)

        print(Samples)
        print('')


        print('ハズレ確率', 100 * np.count_nonzero(Samples == '0') / SampleSize, '[%]')
        print('アタリ確率', 100 * np.count_nonzero(Samples == '1') / SampleSize, '[%]')
        print('')


        SeedMoney = 1000 # 元手 1,000ドル
        Bet = 10 # 掛け金


        MyBet = Bet


        for i in Samples:
            print('元手(前):', SeedMoney, end = ', ')
            print('掛け金:', MyBet, end = ', ')

            if '0' == i:
                print('ハズレ', end = ', ')
                SeedMoney = SeedMoney - MyBet
                MyBet = MyBet * 2
            elif '1' == i:
                print('アタリ', end = ', ')
                SeedMoney = SeedMoney + 2 * MyBet
                MyBet = Bet

            print('元手(後):', SeedMoney)

            if SeedMoney <= 0:
                print('破産!!')
                break

            if SeedMoney < MyBet:
                print('全財産!!')
                MyBet = SeedMoney


        print('')
        print('元手(結果):', SeedMoney)

        # 実験結果をリストに追加
        Results.append(SeedMoney)


    print('')
    print(Results)


    # ヒストグラムを表示
    plt.hist(Results, bins = 40, histtype = 'bar', edgecolor = 'black')
    plt.show()


if __name__ == '__main__':
    main()

ちなみに、掛け金の初期値は10ドルとしました。

上記のPythonプログラムを実行した結果を以下に示します。

第 39 人目
['1' '0' '0' '1' '1' '1' '1' '0' '1' '1' '0' '1' '1' '1' '0' '0' '1' '1'
 '0' '1' '0' '1' '0' '1' '1' '1' '0' '0' '1' '1' '0' '1' '1' '1' '1' '0'
 '0' '0' '1' '0' '1' '1' '0' '0' '1' '1' '1' '1' '0' '1' '0' '1' '1' '1'
 '1' '1' '1' '1' '1' '1' '1' '0' '1' '0' '1' '0' '1' '0' '0' '1' '1' '1'
 '0' '1' '1' '1' '1' '1' '1' '1' '1' '1' '0' '1' '1' '0' '0' '1' '1' '1'
 '1' '1' '1' '0' '1' '0' '0' '0' '1' '0']

ハズレ確率 34.0 [%]
アタリ確率 66.0 [%]

元手(前): 1000, 掛け金: 10, アタリ, 元手(後): 1020
元手(前): 1020, 掛け金: 10, ハズレ, 元手(後): 1010
元手(前): 1010, 掛け金: 20, ハズレ, 元手(後): 990
元手(前): 990, 掛け金: 40, アタリ, 元手(後): 1070
元手(前): 1070, 掛け金: 10, アタリ, 元手(後): 1090
元手(前): 1090, 掛け金: 10, アタリ, 元手(後): 1110
元手(前): 1110, 掛け金: 10, アタリ, 元手(後): 1130
元手(前): 1130, 掛け金: 10, ハズレ, 元手(後): 1120
元手(前): 1120, 掛け金: 20, アタリ, 元手(後): 1160
元手(前): 1160, 掛け金: 10, アタリ, 元手(後): 1180
元手(前): 1180, 掛け金: 10, ハズレ, 元手(後): 1170
元手(前): 1170, 掛け金: 20, アタリ, 元手(後): 1210
元手(前): 1210, 掛け金: 10, アタリ, 元手(後): 1230
元手(前): 1230, 掛け金: 10, アタリ, 元手(後): 1250
元手(前): 1250, 掛け金: 10, ハズレ, 元手(後): 1240
元手(前): 1240, 掛け金: 20, ハズレ, 元手(後): 1220
元手(前): 1220, 掛け金: 40, アタリ, 元手(後): 1300
元手(前): 1300, 掛け金: 10, アタリ, 元手(後): 1320
元手(前): 1320, 掛け金: 10, ハズレ, 元手(後): 1310
元手(前): 1310, 掛け金: 20, アタリ, 元手(後): 1350
元手(前): 1350, 掛け金: 10, ハズレ, 元手(後): 1340
元手(前): 1340, 掛け金: 20, アタリ, 元手(後): 1380
元手(前): 1380, 掛け金: 10, ハズレ, 元手(後): 1370
元手(前): 1370, 掛け金: 20, アタリ, 元手(後): 1410
元手(前): 1410, 掛け金: 10, アタリ, 元手(後): 1430
元手(前): 1430, 掛け金: 10, アタリ, 元手(後): 1450
元手(前): 1450, 掛け金: 10, ハズレ, 元手(後): 1440
元手(前): 1440, 掛け金: 20, ハズレ, 元手(後): 1420
元手(前): 1420, 掛け金: 40, アタリ, 元手(後): 1500
元手(前): 1500, 掛け金: 10, アタリ, 元手(後): 1520
元手(前): 1520, 掛け金: 10, ハズレ, 元手(後): 1510
元手(前): 1510, 掛け金: 20, アタリ, 元手(後): 1550
元手(前): 1550, 掛け金: 10, アタリ, 元手(後): 1570
元手(前): 1570, 掛け金: 10, アタリ, 元手(後): 1590
元手(前): 1590, 掛け金: 10, アタリ, 元手(後): 1610
元手(前): 1610, 掛け金: 10, ハズレ, 元手(後): 1600
元手(前): 1600, 掛け金: 20, ハズレ, 元手(後): 1580
元手(前): 1580, 掛け金: 40, ハズレ, 元手(後): 1540
元手(前): 1540, 掛け金: 80, アタリ, 元手(後): 1700
元手(前): 1700, 掛け金: 10, ハズレ, 元手(後): 1690
元手(前): 1690, 掛け金: 20, アタリ, 元手(後): 1730
元手(前): 1730, 掛け金: 10, アタリ, 元手(後): 1750
元手(前): 1750, 掛け金: 10, ハズレ, 元手(後): 1740
元手(前): 1740, 掛け金: 20, ハズレ, 元手(後): 1720
元手(前): 1720, 掛け金: 40, アタリ, 元手(後): 1800
元手(前): 1800, 掛け金: 10, アタリ, 元手(後): 1820
元手(前): 1820, 掛け金: 10, アタリ, 元手(後): 1840
元手(前): 1840, 掛け金: 10, アタリ, 元手(後): 1860
元手(前): 1860, 掛け金: 10, ハズレ, 元手(後): 1850
元手(前): 1850, 掛け金: 20, アタリ, 元手(後): 1890
元手(前): 1890, 掛け金: 10, ハズレ, 元手(後): 1880
元手(前): 1880, 掛け金: 20, アタリ, 元手(後): 1920
元手(前): 1920, 掛け金: 10, アタリ, 元手(後): 1940
元手(前): 1940, 掛け金: 10, アタリ, 元手(後): 1960
元手(前): 1960, 掛け金: 10, アタリ, 元手(後): 1980
元手(前): 1980, 掛け金: 10, アタリ, 元手(後): 2000
元手(前): 2000, 掛け金: 10, アタリ, 元手(後): 2020
元手(前): 2020, 掛け金: 10, アタリ, 元手(後): 2040
元手(前): 2040, 掛け金: 10, アタリ, 元手(後): 2060
元手(前): 2060, 掛け金: 10, アタリ, 元手(後): 2080
元手(前): 2080, 掛け金: 10, アタリ, 元手(後): 2100
元手(前): 2100, 掛け金: 10, ハズレ, 元手(後): 2090
元手(前): 2090, 掛け金: 20, アタリ, 元手(後): 2130
元手(前): 2130, 掛け金: 10, ハズレ, 元手(後): 2120
元手(前): 2120, 掛け金: 20, アタリ, 元手(後): 2160
元手(前): 2160, 掛け金: 10, ハズレ, 元手(後): 2150
元手(前): 2150, 掛け金: 20, アタリ, 元手(後): 2190
元手(前): 2190, 掛け金: 10, ハズレ, 元手(後): 2180
元手(前): 2180, 掛け金: 20, ハズレ, 元手(後): 2160
元手(前): 2160, 掛け金: 40, アタリ, 元手(後): 2240
元手(前): 2240, 掛け金: 10, アタリ, 元手(後): 2260
元手(前): 2260, 掛け金: 10, アタリ, 元手(後): 2280
元手(前): 2280, 掛け金: 10, ハズレ, 元手(後): 2270
元手(前): 2270, 掛け金: 20, アタリ, 元手(後): 2310
元手(前): 2310, 掛け金: 10, アタリ, 元手(後): 2330
元手(前): 2330, 掛け金: 10, アタリ, 元手(後): 2350
元手(前): 2350, 掛け金: 10, アタリ, 元手(後): 2370
元手(前): 2370, 掛け金: 10, アタリ, 元手(後): 2390
元手(前): 2390, 掛け金: 10, アタリ, 元手(後): 2410
元手(前): 2410, 掛け金: 10, アタリ, 元手(後): 2430
元手(前): 2430, 掛け金: 10, アタリ, 元手(後): 2450
元手(前): 2450, 掛け金: 10, アタリ, 元手(後): 2470
元手(前): 2470, 掛け金: 10, ハズレ, 元手(後): 2460
元手(前): 2460, 掛け金: 20, アタリ, 元手(後): 2500
元手(前): 2500, 掛け金: 10, アタリ, 元手(後): 2520
元手(前): 2520, 掛け金: 10, ハズレ, 元手(後): 2510
元手(前): 2510, 掛け金: 20, ハズレ, 元手(後): 2490
元手(前): 2490, 掛け金: 40, アタリ, 元手(後): 2570
元手(前): 2570, 掛け金: 10, アタリ, 元手(後): 2590
元手(前): 2590, 掛け金: 10, アタリ, 元手(後): 2610
元手(前): 2610, 掛け金: 10, アタリ, 元手(後): 2630
元手(前): 2630, 掛け金: 10, アタリ, 元手(後): 2650
元手(前): 2650, 掛け金: 10, アタリ, 元手(後): 2670
元手(前): 2670, 掛け金: 10, ハズレ, 元手(後): 2660
元手(前): 2660, 掛け金: 20, アタリ, 元手(後): 2700
元手(前): 2700, 掛け金: 10, ハズレ, 元手(後): 2690
元手(前): 2690, 掛け金: 20, ハズレ, 元手(後): 2670
元手(前): 2670, 掛け金: 40, ハズレ, 元手(後): 2630
元手(前): 2630, 掛け金: 80, アタリ, 元手(後): 2790
元手(前): 2790, 掛け金: 10, ハズレ, 元手(後): 2780

元手(結果): 2780

[2780, 3350, 3260, 3070, 2980, 2870, 3230, 3170, 3200, 3080, 2780, 3100, 3000, 3390, 3120, 3040, 2800, 3160, 3270, 2790, 2820, 4140, 3060, 4000, 2850, 2860, 2860, 2840, 2860, 2920, 2820, 2880, 3020, 2840, 3180, 3080, 3060, 3240, 2940, 2780]

上記のログは、40人目(0から39でカウント)のラルフ・ビンスの実験結果を示しています。

初めの0と1で構成されたリストは、ハズレ(0)とアタリ(1)をランダムな並びで100個含んだものです。

リストのハズレ確率が34.0 [%], アタリ確率が66.0 [%]となっています。

上記のPythonプログラムでは、ランダムでアタリとハズレを生成していますので、アタリとハズレの発生確率が期待値からズレることがあります。

ラルフ・ビンスの実験では、ハズレが40%, アタリが60%ですから、40人目に対する発生確率は、ラルフ・ビンスの実験よりも若干ゆるい条件となりました。

その後の出力は、くじ引きに基づく掛け金と元手の推移を表しています。

例えば、「元手(前): 1000, 掛け金: 10, アタリ, 元手(後): 1020」の意味は、次の通りです。

• くじ引き前の元手が1000ドル

• 掛け金が10ドル

• くじ引きの結果はアタリ

• 元手1000ドルに掛け金の2倍である20ドルが加算された結果が1020ドル

最終的な元手は2780ドルとなり、1000ドルから増えているのが確認できます。

最後のリストは、40人の最終的な元手を表しています。

また、40人の最終的な元手をヒストグラムにて表したものが、下記となります。

ラルフ・ビンスの実験(最終的な元手)

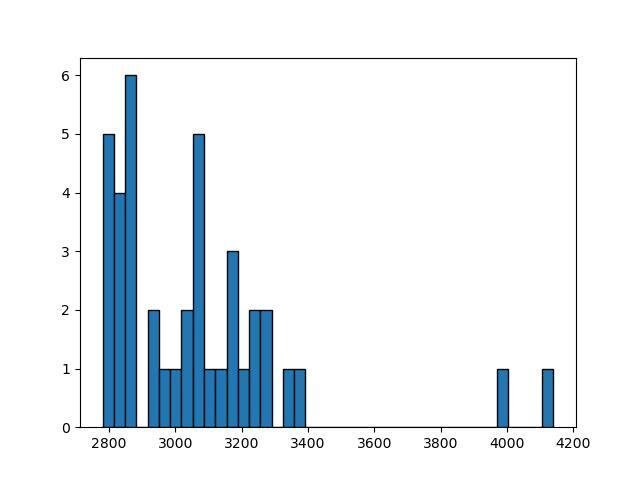
ヒストグラムの横軸は、最終的な元手(単位はドル)です。

また、縦軸は、発生回数(人数)です。

ヒストグラムから、最終的な元手は2800弱～3000ドル強に集中していることが確認できます。

いずれにしても、40人全てで元手の1000ドルを上回りました。

しかし、上記のPythonプログラムを何度も実行すると、元手がゼロになるケースも発生しました。

元手がゼロとなったケースのログの一部を下記に示します。

第 22 人目
['1' '1' '0' '1' '1' '1' '1' '1' '1' '1' '0' '1' '1' '0' '1' '1' '0' '1'
 '1' '1' '0' '0' '0' '1' '0' '1' '0' '0' '1' '0' '0' '0' '0' '0' '0' '0'
 '0' '0' '1' '0' '0' '0' '1' '1' '0' '1' '0' '1' '1' '1' '1' '1' '1' '0'
 '1' '1' '1' '0' '0' '0' '0' '1' '1' '0' '1' '1' '1' '0' '1' '0' '1' '1'
 '1' '1' '1' '0' '0' '0' '0' '0' '1' '0' '0' '1' '1' '0' '0' '0' '1' '1'
 '1' '1' '1' '1' '0' '1' '0' '0' '0' '1']

ハズレ確率 46.0 [%]
アタリ確率 54.0 [%]

元手(前): 1000, 掛け金: 10, アタリ, 元手(後): 1020
元手(前): 1020, 掛け金: 10, アタリ, 元手(後): 1040
元手(前): 1040, 掛け金: 10, ハズレ, 元手(後): 1030
元手(前): 1030, 掛け金: 20, アタリ, 元手(後): 1070
元手(前): 1070, 掛け金: 10, アタリ, 元手(後): 1090
元手(前): 1090, 掛け金: 10, アタリ, 元手(後): 1110
元手(前): 1110, 掛け金: 10, アタリ, 元手(後): 1130
元手(前): 1130, 掛け金: 10, アタリ, 元手(後): 1150
元手(前): 1150, 掛け金: 10, アタリ, 元手(後): 1170
元手(前): 1170, 掛け金: 10, アタリ, 元手(後): 1190
元手(前): 1190, 掛け金: 10, ハズレ, 元手(後): 1180
元手(前): 1180, 掛け金: 20, アタリ, 元手(後): 1220
元手(前): 1220, 掛け金: 10, アタリ, 元手(後): 1240
元手(前): 1240, 掛け金: 10, ハズレ, 元手(後): 1230
元手(前): 1230, 掛け金: 20, アタリ, 元手(後): 1270
元手(前): 1270, 掛け金: 10, アタリ, 元手(後): 1290
元手(前): 1290, 掛け金: 10, ハズレ, 元手(後): 1280
元手(前): 1280, 掛け金: 20, アタリ, 元手(後): 1320
元手(前): 1320, 掛け金: 10, アタリ, 元手(後): 1340
元手(前): 1340, 掛け金: 10, アタリ, 元手(後): 1360
元手(前): 1360, 掛け金: 10, ハズレ, 元手(後): 1350
元手(前): 1350, 掛け金: 20, ハズレ, 元手(後): 1330
元手(前): 1330, 掛け金: 40, ハズレ, 元手(後): 1290
元手(前): 1290, 掛け金: 80, アタリ, 元手(後): 1450
元手(前): 1450, 掛け金: 10, ハズレ, 元手(後): 1440
元手(前): 1440, 掛け金: 20, アタリ, 元手(後): 1480
元手(前): 1480, 掛け金: 10, ハズレ, 元手(後): 1470
元手(前): 1470, 掛け金: 20, ハズレ, 元手(後): 1450
元手(前): 1450, 掛け金: 40, アタリ, 元手(後): 1530
元手(前): 1530, 掛け金: 10, ハズレ, 元手(後): 1520
元手(前): 1520, 掛け金: 20, ハズレ, 元手(後): 1500
元手(前): 1500, 掛け金: 40, ハズレ, 元手(後): 1460
元手(前): 1460, 掛け金: 80, ハズレ, 元手(後): 1380
元手(前): 1380, 掛け金: 160, ハズレ, 元手(後): 1220
元手(前): 1220, 掛け金: 320, ハズレ, 元手(後): 900
元手(前): 900, 掛け金: 640, ハズレ, 元手(後): 260
全財産!!
元手(前): 260, 掛け金: 260, ハズレ, 元手(後): 0
破産!!

元手(結果): 0

アタリとハズレの発生確率に期待値との大きなズレはありません。

しかし、くじ引きのリストを確認するとハズレが9回連続で発生しており、その途中で元手がゼロとなってしまいました。

40人の最終的な元手をヒストグラムにて表したものが、下記となります。

元手ゼロが確認されたケースでのラルフ・ビンスの実験(最終的な元手)

40人中4人が元手ゼロとなっています。

このようなケースに対応するには、掛け金の初期値を現状の10ドルから少額に変更すれば良いです。

例えば、掛け金の初期値を1ドルとした場合、ハズレを連続で引くことで掛け金が2, 4, 8, 16, …と増えていきます。

連続ハズレと元手の関係(掛け金が1ドルの場合)

詳細は、上記の表のようになるのですが、連続9回までのハズレであれば元手がゼロになることはありません。

以上、Pythonプログラムを使ってラルフ・ビンスの実験に対する検証を行いました。

その結果、確かに元手がゼロになるケースは確認されましたが、それは40人中4人でした。

つまり、90%の人が勝ったということです。

また、掛け金を10ドルから1ドルに抑えることで、さらに勝つ人数は増えるはずです。

このため、ラルフ・ビンスの実験に対しては、マーチンゲール法が有効であることが確認できたと私は考えます。
(^_^)ﾔｯﾊﾟﾘﾈ

結果を受けて感じたこと

シゲルさんの教えと、今回行ったラルフ・ビンスの実験に対する検証結果を受けて、改めて私が感じたことは、以下の通りです。

• 投資資金に余裕があれば、ナンピンは有効な投資戦略となる

株式相場の格言では、「下手なナンピン、素寒貧(すかんぴん)」とされています。

しかし、投資資金に余裕があれば、少しずつでもナンピンを実行し、購買単価を下げておき、その後、値上がりしたら少しづつ売っていくのが良いと私は感じました。

ナンピンによって一定の投資資金は拘束されますが、投資資金に余裕があれば問題ありません。

また、ナンピンによって株価が下落した場合は評価損が増えます。

それでも、株価が上昇した際にナンピンした株を購入価格より高い値段で売れば、トータルの損失は減少します。

こうしたことを繰り返すことで、少しずつ損失が減少し、塩漬けが解消されるのではないかと私は考えます。

参考 現役トレーダーシゲルさんの教え

最後に、現役トレーダーシゲルさんの教えに対する、私の価値観と理解に基づくポイントを挙げておきます。

• シゲルさんは2023年で87歳を迎えた現役のデイトレーダーで投資歴は68年

• 1,200銘柄弱を監視対象とし、80銘柄程度に対してデイトレードを実施

• 銘柄選定のポイント

  • 増収、増益、増配

  • 利益は特に経常利益と純利益に注目

  • 企業の成長性を重視

  • 企業のビジネスモデルを理解する必要あり

• 株の売買は「1:2:6」ルールに基づく(詳細は、下記を参照)

• 投資対象は中小型株

• 売買のタイミングはローソク足、テクニカル分析と投資経験に基づく直感で決める

• シゲルさんが参照するテクニカル分析の指標は以下の通り

  • RSI

  • 価格帯別出来高

  • MACD

  • 一目均衡表

  • 新値3本足

• 会社四季報は必須(シゲルさんは会社四季報と同い年)

• 損切りはあまりしない(評価損は2億円以上)

「1:2:6」ルールについて補足です。

私は株を売買するときは、「1:2:6」ルールを意識しています。
「この株はよさそうだ」と思ったら、まず打診買いで1000株程度買ってみて、「やっぱりよさそうだ」と思ったらさらに2000株、「これはいける」と思ったら6000株を購入するというやり方です。売る場合も同じです。

『87歳、現役トレーダー シゲルさんの教え 資産18億円を築いた「投資術」』
「株の売買は「1:2:6」のルール」より

私は、デイトレーダーのシゲルさんがどのようなテクニカル分析の指標を使っているのかに興味がありました。

私にとって新鮮だったのは、新値3本足です。

新値3本足は、本で読んだことがある程度の記憶しかなく、かなりマイナーな指標だと考えていました。

折角ですので、新値3本足について勉強してみようと思いました。