
ピタゴラスは傲慢だった!?数学検定3級から学ぶピタゴラスの定理
数学検定3級シリーズ第2弾。今日は、中学校3年生の最後に習う「三平方の定理(ピタゴラスの定理)」について取り上げます。
というのも、先日宇都宮大学の公開講座「平方根を通して数学を楽しむ 大関清太名誉教授」に参加してきたのですが、その時のテーマが「三平方の定理(ピタゴラスの定理)」だったから。
「平方根を通して数学を楽しむ 大関清太名誉教授」
小学校では算数が好きだったのに中学校から分からなくなった。色々原因があるでしょうが平方根もその一つです。昔の人たちも頭をかかえたのです。平方根を通して現代数学を探ってみましょう。
1)今日の問題

答えは
(16) AB=5√2 (cm)
(17) OH=4√6(cm)
解説
この問題は三平方の定理(ピタゴラスの定理)に関する理解をはかるのがねらいです。
下記の公式は、中学数学の中で絶対に覚えておかなければならない公式の1つ👇
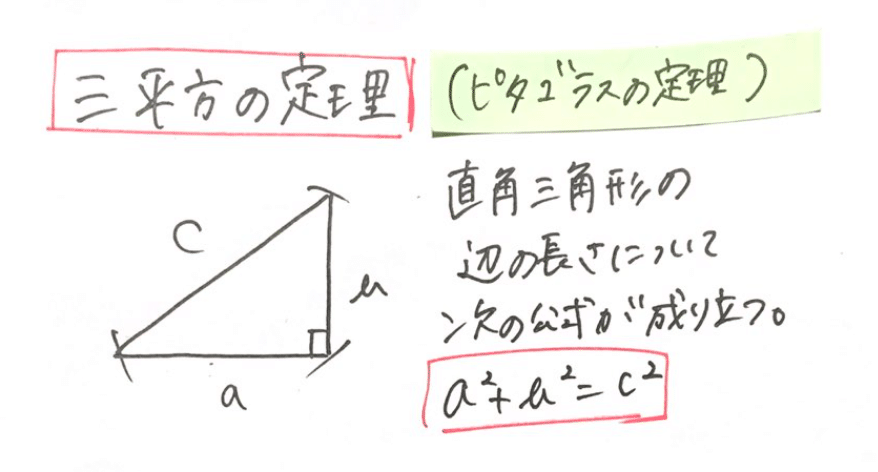
(16)ももちろん三平方の定理を使います👇
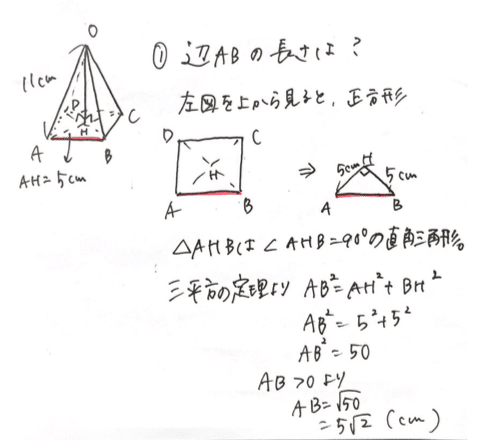

(17)も三平方の定理を使います👇
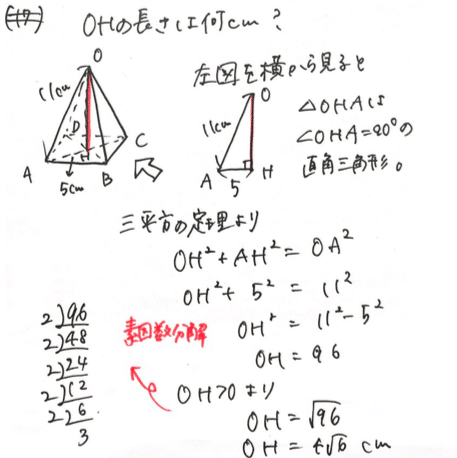
2)三平方の定理(ピタゴラスの定理)の応用
三平方の定理の応用例を1つあげると、建築分野です。建物の図面を描くとき、鉛直と水平の寸法を測ります。たてと横の長さがわかれば、斜めを計らなくても、三平方の定理により斜辺の長さが計算できる、ということです。
3)三平方の定理とピタゴラスの定理、どっちが正解?
三平方の定理とピタゴラスの定理は、どちらも下記の定理を指します。

ではなぜわざわざ別の言い方があるのでしょうか。
ピタゴラスがこの定理を発見したと言われているが、諸説あるため中学校の教科書では「三平方の定理」となっている。
「平方」とは、2乗のことです。「三平方」なので、3つの値の平方をとる、という意味。
4)ピタゴラスとは
ピタゴラスは紀元前570年ごろ、エーゲ海のサモス島で生まれたと言われています。サモス島は当時ギリシャ文明の中心地で神殿や水道工事が盛んに行われていました。
ピタゴラスは、エジプトで勉強しギリシャの都市クロトンに学校を開き、数学・科学・哲学を教えて業績を上げました。
しかし、弟子たちに習ったことを外で喋ることを禁じ弟子の業績も独り占めしたと言われており、最終的には反対派に学校を焼かれ、本人も殺害されてしまったとか。。。
ピタゴラスの定理は、実は名もなき偉人が発見したのかもしれませんね。
ちなみに、ピタゴラスの定理の証明は何百通りもあります。

書籍も発売されていました。
なかなかのお値段。。夏休みにでも挑戦してみようかな。。
最後に。
ーーーーーーーーーー
今日の問題、解けたよ!という方はぜひ「♡スキ」をタップお願いします。難しかったという方も「やってみた!」ということで「♡スキ」をお願いします。また、noteには、クリエイターを応援する機能が満載です。フォローよろしくお願いいたします。演者、スタッフのモチベーションに繋がります。番組で取り上げてほしい事がありましたらコメントもよろしくお願いします!
いいなと思ったら応援しよう!

