
Python3 で世界の出生数を予測をしてみた。時系列データと予測モデル作成[SARIMA]
こんにちは!機械学習を勉強中の身ですが、今回初めて時系列データ分析に挑戦してみました。データは過去50年に及ぶ世界の出生数になります。世界の出生数の各年の変化をみると、興味深いことに出生数が多い月とそうでない月の一定の偏りがみられました。その偏りに周期性(季節変動)があるとして、季節変動データ向けのSARIMAモデルを用いて予測を行いました。
使用環境:Python 3.11.5
データセット:Kaggleにある Seasonal Variation in Births よりダウンロード。約135カ国※ の1967年1月から2021年7月における月別の出生数のデータ。
※ 現在2023年度の世界の国数が約196カ国であることから、世界の全ての国のデータは揃っていないことにご留意ください。ここでは便宜上、「世界のデータ」と述べさせていただきます。
利用するライブラリ
import pandas as pd
from datetime import datetime
import matplotlib.pyplot as plt
import numpy as np
import statsmodels as sm
import statsmodels.api as sm
import itertools
from sklearn.metrics import mean_squared_errorデータの前処理
# データの読み込み
birth_months = pd.read_csv("xxxxxxx/BirthMonthsData.csv", dtype={'x02': 'float64'})
#出力
print(birth_months.head())
53409行7列のデータで構成されています。1967年1月から2021年7月 の54年分にもなります。

必要な情報(Year, Month, Number_of_Births)のみを取り出し、使える形に処理していきます。
まず、いらない列を除きます。
#いらない列の削除
birth_months = birth_months.drop(['Country or Area', 'Area', 'Record Type', 'Reliability'], axis=1)
print(birth_months.head())
#Month列の情報の確認
print(birth_months["Month"].unique())
#['Total' 'January' 'February' 'March' 'April' 'May' 'June' 'July' 'August'
#'September' 'October' 'November' 'December' 'Unknown' 'January - March'
#'April - June' 'July - September' 'October - December']
#月名以外のデータを削除
Months_to_remove = ['Total','Unknown','January - March','April - June','July - September', 'October - December']
for month in Months_to_remove:#一気に全部消す方法がみつからない。。
birth_months = birth_months.drop(birth_months[birth_months['Month'] == month].index, axis=0)
#出力
print(birth_months["Month"].unique())
print(birth_months.head())
'Month' のカラムに'Total'、 'Unknown' 、 'January - March' などの使えないデータがあったため、それらを除いた後、問題なく除かれているか確認しました。
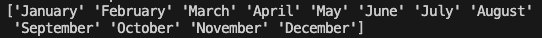
処理後、48581 行3列になりました。
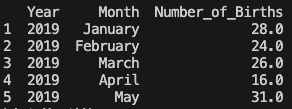
次に Year と Month の列を一つにまとめることで、その後の時系列分析ができるようにします。
#月名を数字に変える関数の作成(Calendar などを用いたもっと効率的なやり方もありそうですが。。)
def MonthToNum(MonthName):
Lists=[]
for i in MonthName:
if i == 'January':
i = '01'
if i == 'February':
i = '02'
~~~
if i == 'November':
i = '11'
if i == 'December':
i = '12'
Lists.append(i)
return Lists
#Month列の月名をリスト化
MonthNames = birth_months['Month'].tolist()
#関数を実行し、リストの月名を数字に変換
MonthNumbers = MonthToNum(MonthNames)
#リストをデータフレーム化し、"Month#" 列として birth_months に追加
birth_months["Month#"] = MonthNumbers
# "Year" と "Month#" の二つの列を結合した新しい "Year_Month" 列を birth_months に作成
birth_months["Year_Month"] = birth_months['Year'].astype(str) + "-" + birth_months["Month#"]
# "Year_Month" 列の数字情報が日付情報として認識されるよう、to_datetime関数で処理
birth_months['Year_Month'] = pd.to_datetime(birth_months['Year_Month'])
# 必要無い列の削除
birth_months = birth_months.drop(['Year', 'Month', 'Month#'], axis=1)
#出力
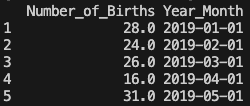
print(birth_months.head())年と月の情報と自動生成された日 "01" の情報が連結された形で出力されました。
時間のデータをインデックスとして指定します。
#"Year_Month" 列をインデックスとして指定
birth_months=birth_months.set_index('Year_Month')
print(birth_months.head())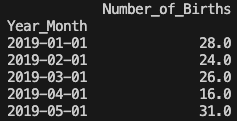
そして、時間 'Year_Month' でグループ化することで、各年月の出生数の合計を算出します。
#'Year_Month' でグループ化し、各グループの合計を算出
birth_months=birth_months.groupby(['Year_Month']).sum().sort_index()
print(birth_months)
データのグラフ化
前処理したデータをグラフ化します。
plt.plot(birth_months)
plt.xlabel('Year')
plt.ylabel('Number of Births')
plt.show()
データ量が多すぎてこのままではグラフが見づらいので、短い期間(2004年1月から2007年1月)に絞って見てみます。
#上記で行ったto_datetime 関数の処理を一旦キャンセルした。でないと、以下のグラフ化がうまくいかなかった。
#birth_months['Year_Month'] = pd.to_datetime(birth_months['Year_Month'])
plt.plot(birth_months)
plt.xlim(['2004-01', '2007-01'])
plt.xlabel('Year')
plt.ylabel('Number of Births')
plt.xticks(['2004-01', '2004-07', '2005-01', '2005-07', '2006-01', '2006-07', '2007-01'],['2004-01', '2004-07', '2005-01', '2005-07', '2006-01', '2006-07', '2007-01'])
plt.grid(True)
plt.show()以下のグラフが示すように、一年の出生数の変動のパターンが各年で似通っていることが分かります。1月から2月にかけてガクッと減少し、10月辺りでピークになる傾向が各年で見られ、ちょうど一年周期で変動していることが分かります。これは世界的な傾向のようで、とても興味深いですね。

なお、関連論文は Proceeding of the National Academy of Sciences (PNAS) の Within-mother analysis of seasonal patterns in health at birth になります。出生月のみならず、妊娠期間、出生体重、出生時の健康にも季節性があることや、母親の社会的地位、経済レベルによっても出産する月に違いがあることなど、興味深い研究結果が記されています。
季節調整済み系列
データの準備が終わったので、データの特徴を分析していきます。
季節変動のあるデータの場合、データのトレンドなどといった季節変動以外の時系列データの動きが見えづらいです。
このような場合、StatsModels の tsa.seasonal_decompose 関数を用いることで、原系列から季節変動を取り除き、原系列をトレンド、季節変動、不規則変動 (残差) のデータに分解してくれます。この季節変動が除かれたデータは、季節調整済み系列と呼ばれます。
birth_months_decompose=sm.tsa.seasonal_decompose(birth_months, extrapolate_trend=12, period=54).plot()
#extrapolate_trend=12 (12 months)
#period=54 (655 data/12 months=54.6 years)
#参考:https://stackoverflow.com/questions/60017052/decompose-for-time-series-valueerror-you-must-specify-a-period-or-x-must-be
plt.show()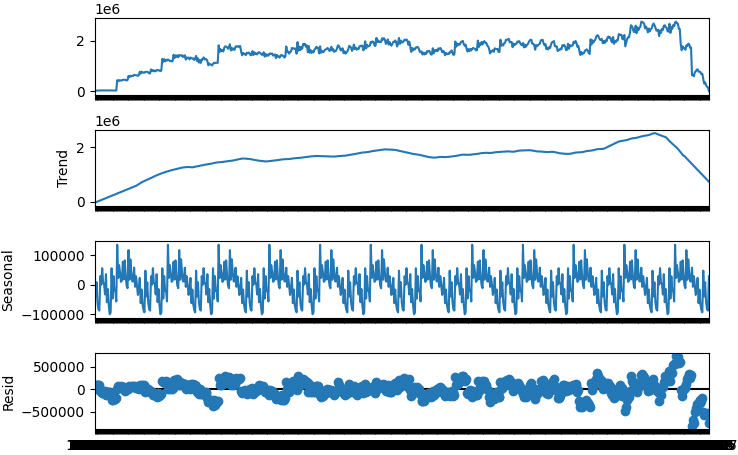
原系列
最初に示したグラフと同様のオリジナルデータです。
トレンド
原系列データの全体の傾向がよく捉えられています。
季節(周期)変動
完璧なまでに揃った美しい季節変動が出てきました。
残差
トレンドと季節変動では説明できない不規則変動のことをいいます。全体的にはバラツキが均等に見えます。
ADF検定
さて、この残差のバラツキが均等であるかどうか、つまり定常性があり、時系列分析に使えるかどうかを調べていきます。そのための一般的な手法としてADF 検定 (Augmented Dickey Fuller test) が用いられます。この検定では、データが単位根過程に従うかどうかで定常性を判断しています。単位根過程の詳細は数学的な説明が必要なのでここでは割愛しますが、要は定常過程に従わず、時系列分析に向かない過程のことを言います。
ADF 検定では、時系列モデルの一つであるAR(Autoregressive: 自己回帰)過程を表す式で使用される『係数が1である単位根過程(=長期的な予測はできない)』を帰無仮説、『係数が1未満である(=定常過程に従い予測可能)』を対立仮説としています。
残差を検定して帰無仮説が棄却された場合は、対立仮説の「定常過程に従う」を採用することになり、時系列モデルを用いた予測が可能だと判断できます。
ADF 検定には、stattools の adfuller 関数を用います。まず、原系列のデータで検定してみます。
# トレンド無し、AR過程の期待値0(定数項無し)
n = sm.tsa.stattools.adfuller(birth_months, regression="n")
# トレンド無し、AR過程の期待値0でない(定数項有り)
c = sm.tsa.stattools.adfuller(birth_months, regression="c")
# トレンド有り(1次)、AR過程の期待値0でない(定数項有り)
ct = sm.tsa.stattools.adfuller(birth_months, regression="ct")
# トレンド有り(一次と二次)、AR過程の期待値0でない(定数項有り)
ctt = sm.tsa.stattools.adfuller(birth_months, regression="ctt")
#結果の出力
print("n:")
print(n[1])
print()
print("c:")
print(c[1])
print()
print("ct:")
print(ct[1])
print()
print("ctt:")
print(ctt[1])
トレンドがある場合のct と ctt の結果に注目すると、値が1に近く帰無仮説を棄却できない、つまり定常性を持たないと判断できます。予想通りの結果です。
次に、差分を取ったデータで同様の検定を行います。階差系列は、時系列データの中の隣り合うデータ同士で引き算していった系列のことです。階差を取ることでトレンドと季節変動を除去することができます。
#差分を取り、ズラすことでできた欠損値を除く
birth_months_diff= birth_months.diff()
birth_months_diff=birth_months_diff.dropna()
# トレンド無し、AR過程の期待値0(定数項無し)
n = sm.tsa.stattools.adfuller(birth_months_diff, regression="n")
# トレンド無し、AR過程の期待値0でない(定数項有り)
c = sm.tsa.stattools.adfuller(birth_months_diff, regression="c")
# トレンド有り(1次)、AR過程の期待値0でない(定数項有り)
ct = sm.tsa.stattools.adfuller(birth_months_diff, regression="ct")
# トレンド有り(一次と二次)、AR過程の期待値0でない(定数項有り)
ctt = sm.tsa.stattools.adfuller(birth_months_diff, regression="ctt")
#結果の出力
print("n:")
print(n[1])
print()
print("c:")
print(c[1])
print()
print("ct:")
print(ct[1])
print()
print("ctt:")
print(ctt[1])
いずれの値も(特に n のトレンド無し、AR過程の期待値 0 の場合で)有意水準より遥かに小さい値となっており、帰無仮説を棄却できるので「定常過程に従う」と判断できます。グラフで見ても以下のように定常性が確認できますね。
plt.plot(birth_months_diff)
plt.show()
今回のケースのように差分を取ることで単位根無しと判定された場合、時系列分析のARIMA(p,d,q)モデルに当てはめて良いことになります!
自己相関関数(ACF:Autocorrelation Function)と偏自己相関関数(PACF:Partial Autocorrelation Function)
自己相関とは、時系列の異なる時点における2つのデータ間の相関のことです。例えば、ある区間で区切られた値の間で、強い正または負の相関を持つ場合、過去の値が現在の値に影響していると言えます。言い換えると、過去のデータとの類似度を表しているとも表現できます。
偏自己相関は自己相関に似ていますが、異なる2つの時点間の相関だけを説明し、それらの間にあるより短いラグを考慮に入れないところが自己相関との違いになります。例えば、ラグ3の偏自己相関ではラグ 1 と 2 を含みません。
自己相関関数と偏自己相関関数を用いることで、時系列のランダム性と定常性、トレンドや季節パターンの有無といった時系列データの特性を知ることができます。
自己相関関数と偏自己相関関数のグラフを作成してみます。
# 自己相関のグラフ
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(birth_months, lags=12, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(birth_months, lags=12, ax=ax2)
plt.show()
自己相関の結果ですが(上の図)、相関係数が初めの1からデータがズレていくにつれ徐々に減少していく美しいパターンが見られました。また暫くの間、データが水色で表されている95%信頼区間より外側に見られています。これは統計的に有意である、つまり「前後のデータで相関が無い」という帰無仮説を棄却できています。
このタイプのパターンは相関がかなり強いことを示しています。直前のデータの誤差の影響を受ける MR (Moving Average 移動平均) モデルに当てはめることができそうです。
偏自己相関(下の図)により、やっと周期変動が見えてきました。水色の部分の外側にある統計的に有意なデータをみると、最初のラグと二つ目のラグデータの相関係数がそれぞれ約1と0.25であり、その後に正と負の相関を交互に示す減衰波が続いています。このようなパターンの場合、季節変動を考慮しない ARIMA (Autoregressive Integrated Moving Average: 自己回帰和分移動平均 )モデルに当てはめるなら、この有意な相関係数の個数からデータの移動平均項が同じ数の次数を持つと判断できるようです。しかし、この交互の波は季節変動によるものと思われるので、同様な判断はしない方が良さそうです。(詳しくないのでこれ以上の考察は止めておきます。)
参考:
Types of Autocorrelation
Some Useful Facts About PACF and ACF Patterns
Autocorrelation and Partial Autocorrelation in Time Series Data
自己相関関数(ACF)
偏自己相関関数(PACF)を解釈する
SARIMAの最適パラメーターの探索
では、いよいよこのデータの特徴を説明するのに相応しいモデルを構築していきます!季節変動があること、及び上述のADF 検定や自己相関関数、偏自己相関関数の結果から、SARIMAモデルに当てはめて未来予測することにしました。
SARIMA (Seasonal AutoRegressive Integrated Moving Average) モデルとは、 AR(Autoregressive: 自己回帰)、MR (Moving Average: 移動平均) 、差分の階数(Difference)のパラメーターを合わせ持つ ARIMA (Autoregressive Integrated Moving Average: 自己回帰和分移動平均) モデルに対し、さらに季節性のパラメーター(季節性自己回帰、季節性階差、季節性移動平均、周期)4つを追加することで季節周期を持つ時系列データにも対応できるようにしたモデルです。
SARIMAモデルは、1季節周期の時点数 s(今回のケースでは12)で差分を取ることで、季節による影響を除去します。差分 s における自己回帰項と移動平均項を導出します。
パラメーターは statmodels ライブラリーの SARIMAX 関数の引数として、(p, d, q), (sp, sd, sq, s) のように指定します。
p: 自己回帰の次数 (直前の p 個の値を用いて予測)
d: 階差の次数 (d 次の階差を取って定常にする)
q: 移動平均の次数 (直前の q 個の値を用いて予測)
sp: 季節性自己回帰の次数
sd: 季節性階差の次数
sq: 季節性移動平均の次数
s: 周期(一周期に含まれる時点の数)
パラメーターを設定する前に、まずデータをトレインデータとテストデータに分割します。トレインデータは、2018年12月より以前の全データに、テストデータは、トレインデータの期間の一部と被るように 2018年1月以降の全てのデータにします。
# テストデータとトレインデータの準備
train_data = birth_months[birth_months.index <= "2018-12"]
test_data = birth_months[birth_months.index >= "2017-1"]
s(周期)のパラメーターは12ヶ月の 12 であることは既に分かっているので、それ以外のパラメーターは自分で設定しなければなりません。
このパラメーターの設定は素人でもできるように、BIC(ベイズ情報量基準)という基準に従って、すべてのパラメーターの組み合わせから最適な組み合わせを自動で探してくれるグリッドサーチを用いてみます。
以下のパラメーター探索のための関数を用いて、実際に最適なパラメーターの組み合わせ(=BICの値が最小である場合のパラメーターの組み合わせ)を探索しました。
# パラメーター探索のための関数
def selectparameter(DATA, s):
p = d = q = range(0, 2)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], s) for x in list(itertools.product(p, d, q))]
parameters = []
BICs = np.array([])
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = sm.tsa.statespace.SARIMAX(DATA,
order=param,
seasonal_order=param_seasonal)
results = mod.fit()
parameters.append([param, param_seasonal, results.bic])
BICs = np.append(BICs, results.bic)
except:
continue
return parameters[np.argmin(BICs)]
# 関数を実行し、最適パラメーターを求める
best_params = selectparameter(train_data, 12)
print('best_params: ', best_params)
いとも簡単に最適パラメーターを得ることができました!d(階差の次数)の 1 の値について、定常化に一次の階差を取る必要があった上述の結果と矛盾しないことを確認できました。
参考:
A Gentle Introduction to SARIMA for Time Series Forecasting in Python
SARIMAで予測
パラメーター値が決まったところで、SARIMA モデルを構築していきます。
# SARIMA モデルの構築
birth_months_sarima = sm.tsa.statespace.SARIMAX(train_data, order=(0, 1, 0), seasonal_order=(1, 1, 1, 12)).fit()
# 予測したい時期を指定し、予測データを取得
pred = birth_months_sarima.predict('2017-01', '2021-7')
# 結果をグラフ化する
plt.plot(train_data)
plt.plot(pred, color="#9467bd", label='pred')
plt.plot(test_data, color='k', label='test')
plt.xlim(['2016-01', '2021-12'])
plt.xlabel('Year')
plt.ylabel('Number of Births')
plt.legend()
plt.show()
2017年から2019年は、テストデータ(黒)と予測データ(紫)がかなりの部分で綺麗に重なっているのがみて取れます。成功です!
ただ、2019年以降はCovid-19 によるパンデミックの影響か実際の出生数と予測データに大きな乖離がみられます。ただそれにしても出生数が少なすぎるのではと疑いました。理由として、データが十分に集まらなかった年もあったのではと考え、各年におけるデータ提供国の数を確認してみました。
# 各年度のデータ提供国の数。前処理前のデータを用いた。
for year in range(1967, 2022):
print(str(year), " : ", len(birth_months.query("Year == " + str(year))["Country or Area"].unique()) + 1)
すると、やはりそのようでデータを提供した国の数が年によって違いがありました。特に初期の1960年、70年代と2019年以降で、数が少ないことが分かります。この確認をもっと最初の段階でしておくべきでした😰
しかしながら、それでも2017年から2019年の予測はうまくいっているようにみえます。その時期の出生数が直前のデータと似ているからでしょうか。全体のデータ数が多いので予測精度がそもそも高いからともいえそうです。
予測精度の検証
どこまで正確に予測できているかをより数学的に説明するため、2017年から2019年の予測データとテストデータを用いて次の値を算出しました。
MSE (Mean Square Error)
平均二乗誤差。統計モデルの予測値と実際の値の距離(残差)を二乗して合計した値。つまり、残差の分散に相当します。
RMSE (Root Mean Square Error)
二乗平均平方根誤差。MSEの平方根を取ったもので、残差の標準偏差に相当します。
MSEとRMSEは、これらの残差がどの程度分散しているかを定量化するため、観察されたデータが予測値の周りにどの程度密接して集まっているかを直感的に理解することができます。
ただこれらの方法は、標準化された値でないゆえ、スケールに影響されやすいという欠点があります。一方、次の決定係数ではこの問題を解決してくれます。
R2(coefficient of determination、 R_squared)
決定係数。データより得られた回帰式が、目的変数の値の変動をどのくらい説明できるかを示す値です。つまり、推定した回帰式のデータに対する当てはまりの良さを表しています。R二乗は適合度を表す相対的な尺度(パーセンテージ)で表されます。
予測データ、テストデータをそのまま使ってMSEとRMSEを求めると、スケールが大きすぎたため、値が非常に大きい値か無限大になってしまいました。よって、各データを10の4乗(1万人)で割ってから、求め直しました。
# 予測データ、テストデータを2017-18に絞ってから、10**6で割る
pred = pred[pred.index >= "2017-1"][pred.index <= "2018-12"]
pred = pred/10**6
test_data = test_data[test_data.index >= "2017-1"][test_data.index <= "2018-12"]
test_data = test_data/10**6
#MSE, RMSE, and R^2
mse = mean_absolute_error(test_data, pred)
rmse = np.sqrt(mse)
rxr =r2_score(test_data, pred)
print("MSE: " + str(mse))
print("RMSE: " + str(np.sqrt(mse)))
print("R^2: " + str(rxr))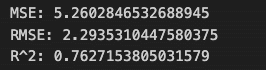
予測データが 219.0 (x 10^4) ~ -278.0 (x 10^4) の範囲内にあることを考えると、MSE と RMSE の値はかなり小さく、残差の分散が非常に小さいことが分かります。
決定係数 R^2 も 0.76 と大きな値で、予測精度もかなり高かったといえます。
このように季節変動がある出生数のデータを用いて、将来の出生数を SARIMAモデルで予測できることを確認できたことは意義があったと思います。パンデミック等の予測不可能な事態や、データの入手等の問題がなければ、同モデルを用いた出生数の未来予測は可能だと思われます。
今後、世界規模で少子高齢化が進むといわれています。これは信頼度の高い予測のようですので、将来の出生数の予測も難しくはないのでしょう。個人的には、少子高齢化先進国の日本がロールモデルとして世界に果たす役割が今後増していく気がしています。
参考:
Root Mean Square Error (RMSE) Statistics By Jim
WORLD SOCIAL REPORT 2023: LEAVING NO ONE BEHIND IN AN AGEING WORLD by United Nations
世界の出生率、驚異的な低下 23カ国で今世紀末までに人口半減=米大学予測
対数系列でもやってみた(おまけ)
データの値の変動が大きい場合、分散を均一にして変動を穏やかにするために、データを対数に変換することがあります。変換されたデータを対数系列と言います。
今回使用した原系列のデータも、自然対数により対数系列にすることで結果に差があるのかを検討することにしました。結論としては、原系列の場合よりやや精度が下がったものの、ほとんど原系列と同様の予測ができました。ご興味があれば、以下の結果もご覧ください。(コードは上述したものと違う場合のみ掲載しました)
原系列を対数に変換
birth_months_log = np.log(birth_months)
plt.plot(birth_months_log)
plt.xlabel('Year')
plt.ylabel('Number of Births')
plt.show()

原系列と比較して、対数系列のグラフがより均一になっているのが分かります。
自己相関関数と偏自己相関関数(対数系列)

原系列を用いた場合と結果が似ています。
ADF 検定(対数系列)

原系列の時と同様、単位根があるという帰無仮説を棄却できず。
次に対数系列の差分で検定を行いました。
#差分を2回取る
birth_months_log_diff= birth_months_log.diff()
birth_months_log_diff= birth_months_log_diff.diff()
birth_months_log_diff=birth_months_log_diff.dropna()
#グラフ化
plt.plot(birth_months_log_diff)
plt.show()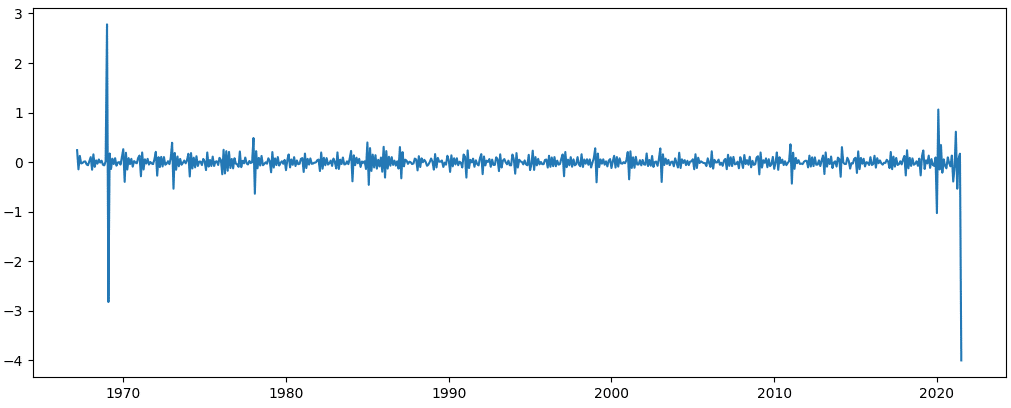

差分を2回取ることで、やっと帰無仮説を棄却できました。単位根無し、2次の階差系列は定常であると言えました。
SARIMAの最適パラメーターの探索(対数系列)
SARIMAモデル構築のための最適パラメーターを、BICを用いて決定しました。
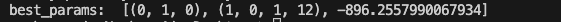
SARIMAモデルの構築(対数系列)
決定したパラメーター値を用いて、SARIMAモデルを構築しました。

原系列の時と同様、2017年から2018年でテストデータと予測データが綺麗に重なっています。
予測精度の検証(対数系列)
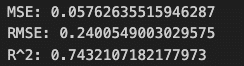
予測データの値が14.5 ~ 14.9 であることを考えると、MSE、RMSEの値はかなり小さく、残差の分散が小さいことが分かります。R2は 0.74と、原系列の0.76より値は少し低いものの、それでもかなり高い予測精度です。
対数系列によるSARIMAモデルを対数無しに変換
上述のモデル構築に用いた対数系列のデータを np.exp() 関数で対数無しに変換し、グラフにしてみました。原系列データで予測した場合と違いがあるか、確認してみました。
#対数系列を原系列にする
train_data = np.exp(train_data)
pred=np.exp(pred)
test_data=np.exp(test_data)
#グラフで表示
plt.plot(train_data)
plt.plot(pred, color="#9467bd", label='pred')
plt.plot(test_data, color='k', label='test')
plt.xlim(['2016-01', '2021-12'])
plt.xlabel('Year')
plt.ylabel('Number of Births')
plt.legend()
plt.show()

両者の違いがほとんど確認できません。
予測精度の検証(対数系列→対数無し)
対数無しに変換したデータでも2017年−2018年の予測精度を検証してみました。
※ スケールが大きすぎるので、10の4乗(1万人)で割った値を用いました。
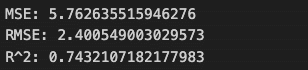
予測データの値が211 (x 10^4) ~ 280 (x 10^4)の範囲にあることから、MSE、RMSEで示される残差の分散は非常に小さいことが分かります。R2は、スケールの影響を受けないので変換前と同じ値ですね。
これらの結果から、原系列を用いた場合と対数系列を用いた場合とでは、予測精度にほとんど違いが無いことが分かりました。今後、変動が大きいデータを扱うことがあれば、安心して対数変換しようと思います。
最後に
時系列解析初心者ながら分析結果を纏めさせていただきました。もし、訂正すべき点やアドバイスなどあればご指摘いただければ幸いです。
拙い解析でしたが、最後までお読みいただきありがとうございました!
