
機械学習で創薬探索のプロセスをかじってみました(パート2:探索的データ分析)
バイオインフォマティクスに疎い私ですが、創薬探索のプロセスを経験すべく、機械学習で化合物のデータを用いた分析をしてみました!
パート1に引き続き、Data Professor という名前でユーチューバーをされているタイ人でバイオインフォマティクスの元准教授の Chanin Nantasenamatさんのビデオ Bioinformatics Project from Scratch - Drug Discovery Part 2 (Exploratory Data Analysis) の内容をご紹介します。説明欄にビデオで使用されているコードのリンクも掲載されています。なお、ここで記述したコードは、自らがやりやすいように一部変更を加えていますのでご了承下さい。
パート1のリンクはこちら
目的
薬剤候補化合物による、エストロゲン受容体 α1(estrogen receptor alpha 1)に対する阻害活性を推測するための機械学習モデルを構築する。
概要
ChEMBL データベースより抽出・前処理した、エストロゲン受容体 α1(estrogen receptor alpha 1) に対する阻害活性が調べられている化合物のデータに対して、その化学的特徴が経口薬として相応しいか否かをリピンスキーの法則を基にして検討する。
分析結果を図で可視化する。また、阻害活性があるグループとそうでないグループ間の差が統計的に有意であるか否かを検討する。
開発環境
MacBook Air
Google Colaboratory
Python 3.6.9
ライブラリとデータの準備
condaと rdkit のインストール
RDkit は、ケモインフォマティクスの分野で用いられる代表的なオープンソースのライブラリで、化合物の構造や性質などの分析が可能です。今回は、化学構造の情報(canonical smiles)などから化学的性質を予測します。RDkit の詳細は以下の記事をご覧ください。
condaと rdkit をインストールします。
! wget https://repo.anaconda.com/miniconda/Miniconda3-py37_4.8.2-Linux-x86_64.sh
! chmod +x Miniconda3-py37_4.8.2-Linux-x86_64.sh
! bash ./Miniconda3-py37_4.8.2-Linux-x86_64.sh -b -f -p /usr/local
! conda install -c rdkit rdkit -y
import sys
sys.path.append('/usr/local/lib/python3.7/site-packages/')前回作成した前処理後のデータの読み込み
詳細はパート1をご覧ください。
import pandas as pd
df = pd.read_csv('estrogenRa_bioactivity_preprocessed_data.csv')
df
化合物以外の情報の削除
ビデオでは以下のコードは存在しなかったのですが、掲載されていたコードのリンクには載っていました。canonical_smiles カラムの化合物のSMILES 表記の情報をピリオド ”.” でスプリットし、長い方を採用するというコードになっています。何をしているのか自分のデータで確認したところ、どうやらこのようなピリオドを挟んで繋がっているCl、 Brなどの混合物を除く処理であることが分かりました。
CCOC(=O)c1cc2ccccc2n1CCN(CC)CC.Cl
Br.C=CCOC(C)C1=CC(C)(C)Nc2ccc(-c3cc(F)ccc3OC)cc21
# canonical_smiles カラムを除く
df_no_smiles = df.drop(columns='canonical_smiles')
# canonical_smiles カラム中の化合物以外の情報を除く
smiles = []
for i in df.canonical_smiles.tolist():
cpd = str(i).split('.')
cpd_longest = max(cpd, key = len)
smiles.append(cpd_longest)
# smiles のリストを canonical_smiles カラムとしてデータフレーム列に変換
smiles = pd.Series(smiles, name = 'canonical_smiles')
# canonical_smiles カラムを除いたデータフレーム df_no_smiles に アップデートした化合物の情報を持つ canonical_smiles カラムを結合
df_clean_smiles = pd.concat([df_no_smiles,smiles], axis=1)
df_clean_smiles
化合物が経口薬に相応しいか検討
リピンスキーの法則
リピンスキーの法則(Lipinski's Rule)とは、ファイザー社の科学者であるクリストファー・リピンスキーによって提唱された、化合物の薬効を評価するための法則です。この薬効は、薬物動態プロファイルとして知られている体内への吸収、分布、代謝、排泄(ADME)のデータに基づいて評価されています。
FDAが承認したすべての経口活性医薬品を分析して得たリピンスキーの法則は、以下になります。この法則に当てはまる化合物は経口薬の候補に相応しいといった指標が得られるのです(あくまでも大雑把な指標にすぎませんが)。
分子量が500ダルトン以下
オクタノール/水分配係数(LogP)が5.0以下 ※ 値が大きほど疎水性大
水素結合供与体 (NHとOHの合計数) が5以下
水素結合受容体 (NとOの合計数) が10以下
お気づきの通り、5の倍数が多いですね。そのため、ルール・オブ・ファイブとも呼ばれているようです。
この法則の詳細については以下の記事などが参考になります。
では、実際に化合物のSMILES データをリピンスキーの法則に照らして評価してみましょう。
numpy 及び rdkit のインポート
import numpy as np
from rdkit import Chem
from rdkit.Chem import Descriptors, Lipinskilipinski 関数の実行
以下の論文を参考にして作られたというlipinski 関数を実行します。
def lipinski(smiles, verbose=False):
# SMILES 表記のデータを rdkit が分析できる形式に変換
moldata= []
for elem in smiles:
mol=Chem.MolFromSmiles(elem)
moldata.append(mol)
baseData= np.arange(1,1) # array([], dtype=int64). 空のアレイの作成
i=0
for mol in moldata:
desc_MolWt = Descriptors.MolWt(mol)
desc_MolLogP = Descriptors.MolLogP(mol)
desc_NumHDonors = Lipinski.NumHDonors(mol)
desc_NumHAcceptors = Lipinski.NumHAcceptors(mol)
row = np.array([desc_MolWt,
desc_MolLogP,
desc_NumHDonors,
desc_NumHAcceptors])
# 4種類のデータが入ったアレイ同士を縦方向に連結する
if(i==0):
baseData=row
else:
baseData=np.vstack([baseData, row])
i=i+1
columnNames=["MW","LogP","NumHDonors","NumHAcceptors"]
descriptors = pd.DataFrame(data=baseData,columns=columnNames)
# moldataの表示
print(moldata)
return descriptors
# lipinski 関数の実行
df_lipinski = lipinski(df_clean_smiles.canonical_smiles)
df_lipinskimoldata の出力 (化合物が Mol オブジェクトとして扱われます。原子の情報が格納されていて、処理速度を上げるため C言語で処理されるようです。)
[<rdkit.Chem.rdchem.Mol object at 0x7f009a201a80>, <rdkit.Chem.rdchem.Mol object at 0x7f009a201c10>, <rdkit.Chem.rdchem.Mol object at 0x7f009a201df0>, <rdkit.Chem.rdchem.Mol object at 0x7f009a201f80>, …..]

無事、リピンスキーの法則の4種類の特徴の情報が得られました!
次に、このリピンスキーのデータフレームと前述の df_clean_smiles を結合させます。
df_combined = pd.concat([df_clean_smiles,df_lipinski], axis=1)
df_combined
IC50 から pIC50への変換
IC50のデータの分布をより均一にするために、つまり IC50値をより扱いやすくするために、IC50を負の対数スケール -log10(IC50)に変換します。
pIC50関数
この処理はカスタム関数 pIC50()で行います。具体的には、次のような手順になります。
1) standard_value カラムの IC50 値を 10の-9 乗(10**-9) 倍することによって nM (ナノモル)から M (モル)に変換 。
2) M値を -log10 に変換。
3) standard_value カラムを削除し、新たに pIC50 カラムを作成。
import numpy as np
def pIC50(input):
pIC50 = []
for i in input['standard_value_norm']:
molar = i*(10**-9) # IC50 値を nM から M に変換
pIC50.append(-np.log10(molar)) # -log10 に変換
input['pIC50'] = pIC50 # pIC50 カラムを追加
x = input.drop('standard_value_norm', 1) #IC50 の情報を除く
return xなぜ対数に変換するかに関しては、以下の記事の説明が参考になりそうです。個人的には、同じく対数で表すpH(ペーハー)=−log[H+] で考えると分かりやすいかと思います。pH2 と pH3 では H+の濃度が10倍違いますが、10の-2乗と10の-3乗と書くより2と3の方がシンプルですし、数字が大きいほど濃度が低い(阻害活性が高い)と一瞬で理解できます。
IC50値の標準化
この関数をすぐ使いたいところですが、その前にもう一つ関数が必要です。それは以下のように IC50値が 100,000,000(10 の 8乗)より大きくなった場合、pIC50値がマイナスになってしまうので、この値を超えないようする関数 norm_value()も準備します。
-np.log10( (10**-9)* 100000000 )
-np.log10( (10**-9)* 10000000000 )1.0
-1.0
def norm_value(input):
norm = []
# 100000000 を超える値は100000000に変換し、マイナスにならないようにする。
for i in input['standard_value']:
if i > 100000000:
i = 100000000
norm.append(i)
input['standard_value_norm'] = norm
x = input.drop('standard_value', 1)
return x
IC50のデータに100,000,000(10の8乗)を超える値があるかどうかは、describe() でチェックできます。私のデータはmax が e+06となっているので実際にこの処理をする必要はないようですが…
df_combined.standard_value.describe()
ここでは norm_value 関数を実行します。
df_norm = norm_value(df_combined)
df_norm
pIC50関数の実行
そして、いよいよ pIC50関数を実行します。
df_final = pIC50(df_norm)
df_final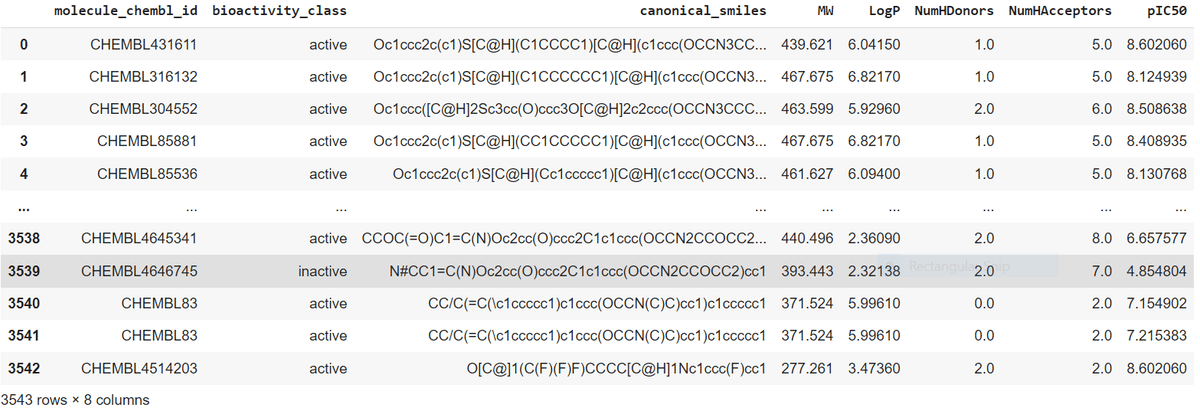
pIC50に置き換わっているのを確認できたところで、データを保存します。
df_final.to_csv('estrogenRa_bioactivity_data_pIC50.csv')探索的データ分析(Exploratory Data Analysis)
取得したデータを図で可視化して、結果を検証してみます。
必要なライブラリーのインポート
import seaborn as sns
sns.set(style='ticks')
import matplotlib.pyplot as plt各阻害活性レベル の割合
各阻害活性レベル (active, intermediate, inactive) の化合物数を棒グラフで表しました。阻害活性レベルの分類の詳細はパート1をご覧ください。
plt.figure(figsize=(5.5, 5.5))
sns.countplot(x='bioactivity_class', data=df_final, edgecolor='black')
plt.xlabel('Bioactivity class', fontsize=14, fontweight='bold')
plt.ylabel('Frequency', fontsize=14, fontweight='bold')
plt.savefig('plot_bioactivity_class.pdf')
阻害活性のある(active)化合物が全体の半分以上を占めていますね。
MW 対 LogP の散布図
化合物の分子量(MW) と疎水性 (LogP) の関係をプロットしました。
plt.figure(figsize=(5.5, 5.5))
sns.scatterplot(x='MW', y='LogP', data=df_final, hue='bioactivity_class', size='pIC50', edgecolor='black', alpha=0.7)
plt.xlabel('MW', fontsize=14, fontweight='bold')
plt.ylabel('LogP', fontsize=14, fontweight='bold')
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0)
plt.savefig('plot_MW_vs_LogP.pdf')
リピンスキーの法則に照らし合わせると(LogP 5以下、MW500以下)、多くの化合物、特にactiveなものに法則に従っていない化合物が多くありました。
pIC50のプロット
各活性レベルとpIC50の関係を箱ひげ図としてプロットします。
plt.figure(figsize=(5.5, 5.5))
sns.boxplot(x = 'bioactivity_class', y = 'pIC50', data = df_final)
plt.xlabel('Bioactivity class', fontsize=14, fontweight='bold')
plt.ylabel('pIC50 value', fontsize=14, fontweight='bold')
plt.savefig('plot_ic50.pdf')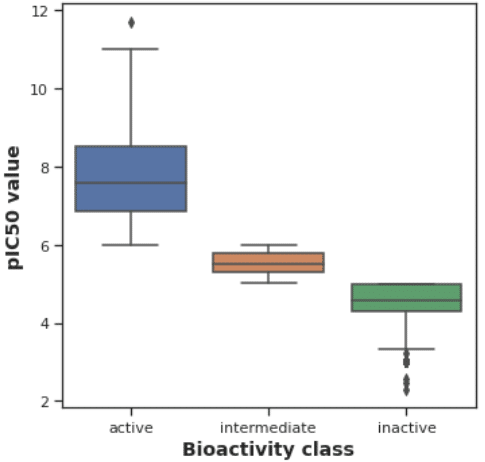
もともと pIC50値によってこれらのグループに分類しましたが(パート1をご参照ください)、その通りに綺麗に分かれています。
マン・ホイットニーのU検定(Mann-Whitney U Test)
次に、pIC50 の activeと inactive のデータのグループが、統計的に差があるかどうかをマン・ホイットニーのU検定で調べます。
マン・ホイットニーのU検定とは、独立した2グループのデータ同士を比較するスチューデントt 検定のノンパラメトリック版である。
2つのサンプルを組み合わせて、値の小さい順に順位付けを行う。そして、2つのサンプルの値が順位付けによってにランダムに混在しているのか、若しくは端に集まっているのかを判断する。ランダムである場合は2つのサンプルに違いがないということであり、同じサンプルの値が集まっている場合は、2つのサンプルに違いがあるということになる。
私と同様、t 検定の方が馴染みがある方も多いかと思いますが、この検定ではt 検定と異なり、並べたデータの順番の番号を用いて計算しています。以下の記事は、U検定を例を用いて解説していて分かりやすいです。
検定の説明はこれくらいにして、 mannwhitney 関数を準備します。
def mannwhitney(descriptor, verbose=False):
from numpy.random import seed
from numpy.random import randn
from scipy.stats import mannwhitneyu
# 乱数の生成
seed(1)
# active と inactive のデータから、検定したい化合物の特徴のデータを取得
selection = [descriptor, 'bioactivity_class']
df = df_final[selection]
active = df[df['bioactivity_class'] == 'active']
active = active[descriptor]
selection = [descriptor, 'bioactivity_class']
df = df_final[selection]
inactive = df[df['bioactivity_class'] == 'inactive']
inactive = inactive[descriptor]
# active と inactive データの比較
stat, p = mannwhitneyu(active, inactive)
#print('Statistics=%.3f, p=%.3f' % (stat, p))
# 出力の形式を指定
alpha = 0.05 # 確率 p が有意水準 alpha より小さいと「二つのグループが同じである」という仮説を否定できる。つまり統計的にこれらのグループは異なると言える。
if p > alpha:
interpretation = 'Same distribution (fail to reject H0)'
else:
interpretation = 'Different distribution (reject H0)'
results = pd.DataFrame({'Descriptor':descriptor,
'Statistics':stat,
'p':p,
'alpha':alpha,
'Interpretation':interpretation}, index=[0])
filename = 'mannwhitneyu_' + descriptor + '.csv'
results.to_csv(filename)
return resultspIC50のU検定
それでは実際に、pIC50 データで active と inactive を比較します。
mannwhitney('pIC50')
確率 p が有意水準 alphaより小さいどころか 0 になっています。よって pIC50 の active と inactive グループは統計的に全く異なるグループであると言えます。
同様にリピンスキーの関数で取得した他の特徴のデータでも見てみましょう。
分子量MW のプロットとU検定
plt.figure(figsize=(5.5, 5.5))
sns.boxplot(x = 'bioactivity_class', y = 'MW', data = df_final)
plt.xlabel('Bioactivity class', fontsize=14, fontweight='bold')
plt.ylabel('MW', fontsize=14, fontweight='bold')
plt.savefig('plot_MW.pdf')
分子量はどのグループもactive が他のグループより少し高いくらいで近いですね。
mannwhitney('MW')
しかし、p が alpha よりかなり小さく、よってMWの active と inactive グループは統計的に違うグループであると言えます。
オクタノール/水分配係数(疎水性) LogP のプロットとU検定
plt.figure(figsize=(5.5, 5.5))
sns.boxplot(x = 'bioactivity_class', y = 'LogP', data = df_final)
plt.xlabel('Bioactivity class', fontsize=14, fontweight='bold')
plt.ylabel('LogP', fontsize=14, fontweight='bold')
plt.savefig('plot_LogP.pdf')
active のグループの方が他のグループより疎水性がやや高くなっています。
mannwhitney('LogP')
p が alpha より非常に小さく、よって LogP の active と inactive グループは統計的に違うグループであると言えます。
水素結合供与体 NumHDonors のプロットとU検定
plt.figure(figsize=(5.5, 5.5))
sns.boxplot(x = 'bioactivity_class', y = 'NumHDonors', data = df_final)
plt.xlabel('Bioactivity class', fontsize=14, fontweight='bold')
plt.ylabel('NumHDonors', fontsize=14, fontweight='bold')
plt.savefig('plot_NumHDonors.pdf')
水素結合供与体の数はどのグループもほぼ同じにみえますが、データのばらつきも非常に小さいです。
mannwhitney('NumHDonors')
p が alpha より非常に小さく、よって水素結合供与体 の active と inactive グループは統計的に違うグループであると言えます。
水素結合受容体 NumHAcceptors のプロットとU検定
plt.figure(figsize=(5.5, 5.5))
sns.boxplot(x = 'bioactivity_class', y = 'NumHAcceptors', data = df_final)
plt.xlabel('Bioactivity class', fontsize=14, fontweight='bold')
plt.ylabel('NumHAcceptors', fontsize=14, fontweight='bold')
plt.savefig('plot_NumHAcceptors.pdf')
inactive グループでほかのグループより水素結合受容体の数がやや大きくなっています。リピンスキーの法則では10個以下となっていて数自体は問題なさそうです。
mannwhitney('NumHAcceptors')
p が alpha より非常に小さく、よって水素結合受容体 の active と inactive グループは統計的に違うグループであると言えます。
結果をまとめますと、
1)active のグループに属する化合物は全体の半数以上と多くみられましたが、MW 対 LogP のスキャッタープロットによりactive なものの中にもリピンスキーの法則から外れているもの(化学的性質が経口薬として相応しくないと推定されるもの)も多くありました。
2)マン・ホイットニーのU検定により、リピンスキーのすべての項目において、active と inactive のグループに統計的に有意な差がみられました。
Zip ファイルの作成
上述のプロットのコードに plt.savefig('plot_NumHAcceptors.pdf') などと書かれているのに気づかれたかもしれませんが、これは実は今回作成した csv ファイルおよび pdf ファイルをまとめてZip ファイルとして保存するためだったのです。論文作成などの際にも使えますし、大変便利です!
! zip -r results.zip . -i *.csv *.pdf

最後に
探索的データ分析がどのようなものか、大体のイメージがつかめたのではないでしょうか。
次回のパート3では、いよいよエストロゲン受容体 α1(estrogen receptor alpha 1)に対する阻害活性を推測するための機械学習モデルを構築します!
