
Stormworksで学ぶ!3DCG入門
この記事は Stormworks 第1 Advent Calendar 2024 第13日目 の記事です。
(※UnityやBlenderの話ではないよ)
ストワのLuaで3DCGできたら面白いよね。そう思ったので書いてみました。
はじめに
この記事では初心者の方から上級者の方まで楽しめるよう、初期のワイヤーフレームから近代的なライティング処理まで4段階のレベルに分けて進めていきます。

3DCGってなんだかやたらと難しそうなイメージがありますが大丈夫!本記事は基本的に高校までの教科書の内容だけを使い、最短距離でライティング処理までたどり着ける構成になっています。
読み終わるころにはStormworksで3DCGを自在に操れるようになっているはず。3DCG技術を習得して凄腕ワーカーになろう!
(Level 1)ワイヤーフレームで立方体を作ってみよう
突然ですが皆様、ワイヤーフレームって知ってますか?
こういうやつです。
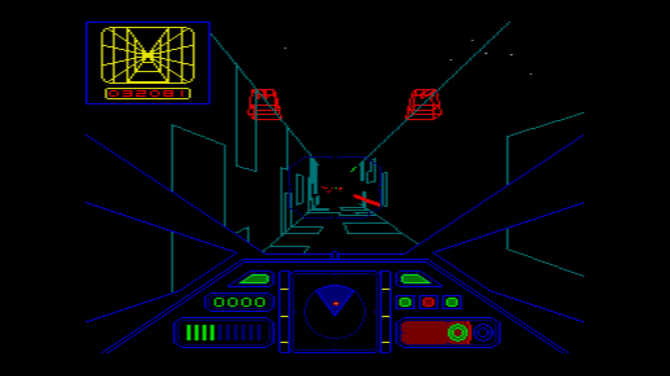
三次元物体の辺のみを描画することで3Dを再現する手法で、人類が初めて手にした3DCG技術でもあります。
過去の遺物と侮るなかれ、30年ほど前までは世界最先端の分野でもバリバリ使われていた由緒正しき手法なんです。(ロッキードF-117攻撃機やノースロップYF-23戦闘機も設計の一部にワイヤーフレームを用いているよ)
爆発的に発展するコンピュータ業界を長きにわたって支えた技術をストワでも再現してみましょう。
(1) 仕様の決定
そもそも3次元の物体をなぜ二次元のモニターで表現できるのでしょうか?それは三次元物体を二次元に投影しているからなんです。
下の図を見ると何となく理解できる人も多いかな?
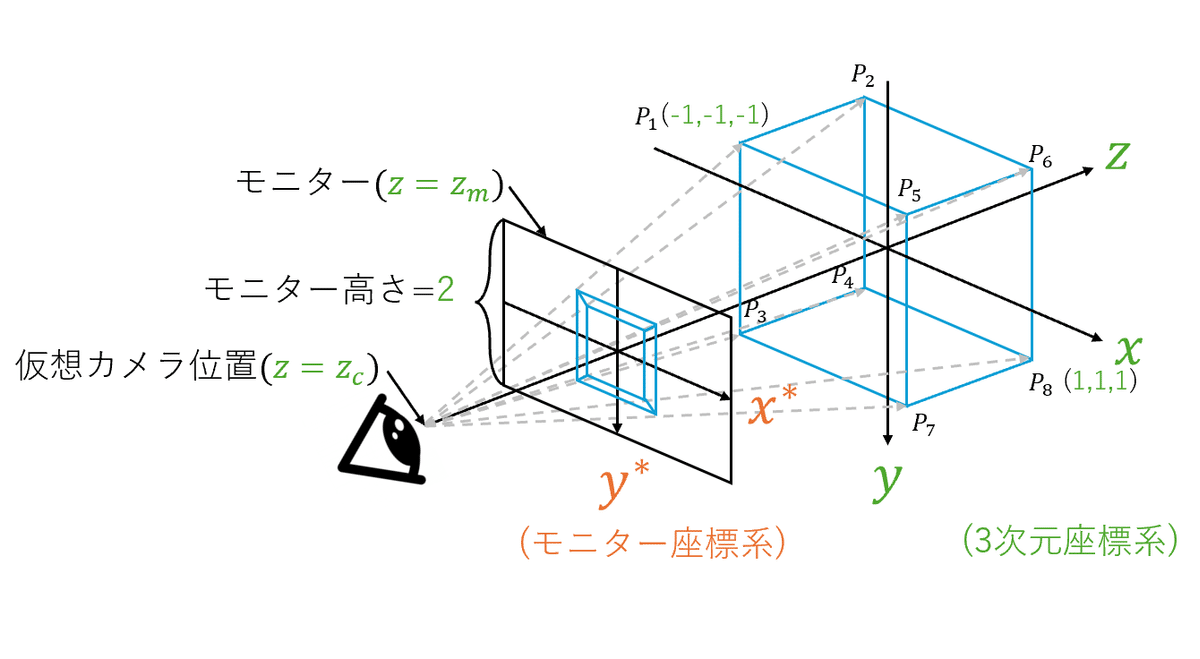
ストワのモニターに合わせた都合上、座標系の向きに注意
このように, ワイヤーフレームを使った3DCGは
・視点 (仮想カメラ位置) と物体の頂点を結び、頂点がモニター座標系でどこに来るか求める
・ペアとなる頂点の番号をもとに、モニター上で頂点同士を結ぶ
という2段階を経て描画が行われているんです。(モニター上の頂点の座標は相似を使って求められるよ)
ということは、
・頂点の三次元空間座標
・ペアとなる頂点の番号
を格納した2つのテーブルがあれば、行けそうな気がしてきませんか?
というわけで、早速作っていきましょう。
(2) 頂点の描画
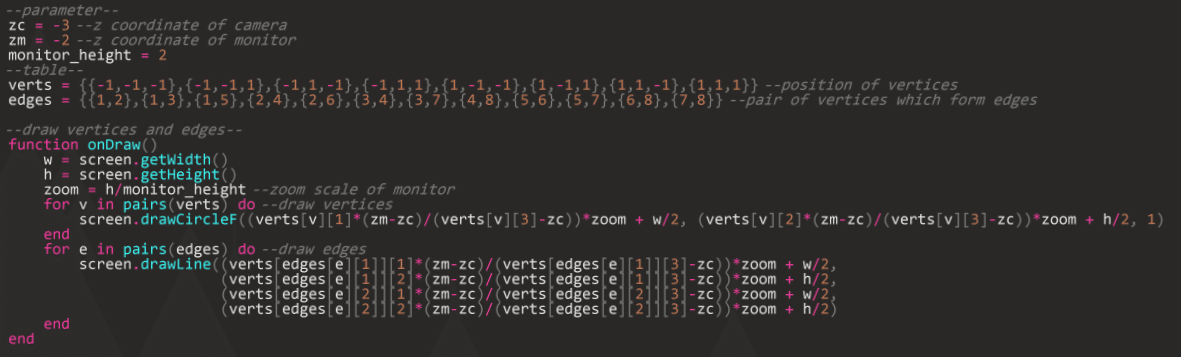
まずは頂点の座標を格納したテーブル (verts)、ペアになる頂点番号を格納したテーブル (edges) を作ります。フォーマットはこんな感じ。
今回は立方体を描画するので頂点は8個、辺は12本あります。

”verts”が頂点座標を、"edges"がペアになる頂点番号をそれぞれ格納。
テーブルができたら、次は実際に描画を行っていきましょう。今回は$${zc=-3, zm=-2,}$$ モニター高さ$${=2}$$としました。
ちなみに、モニター上の頂点の座標の求め方(座標変換)はこんな感じ。
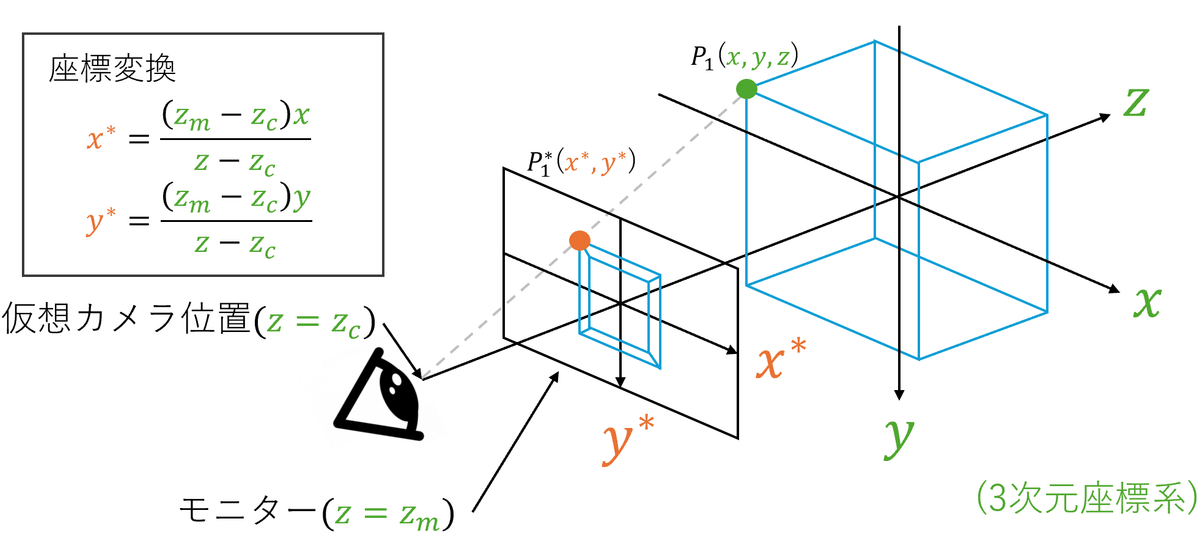
これで準備が整ったので、早速実装していきます!
まずは正しく計算できているか確認のため、頂点のみ描画してみます。コードは画像を参照。(Lua上ではモニター座標はピクセル数で指定することに注意!)
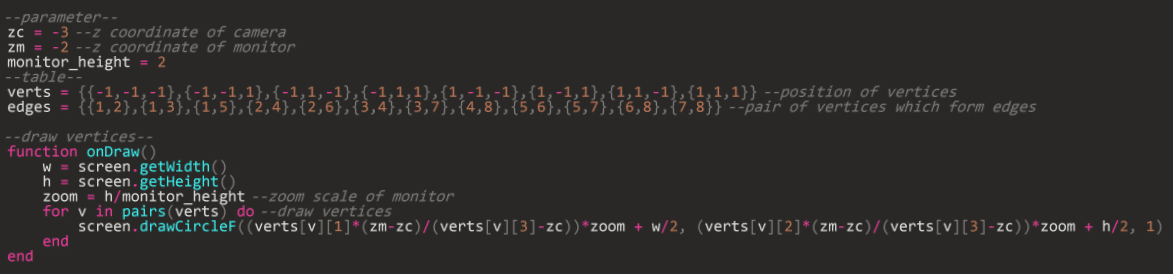
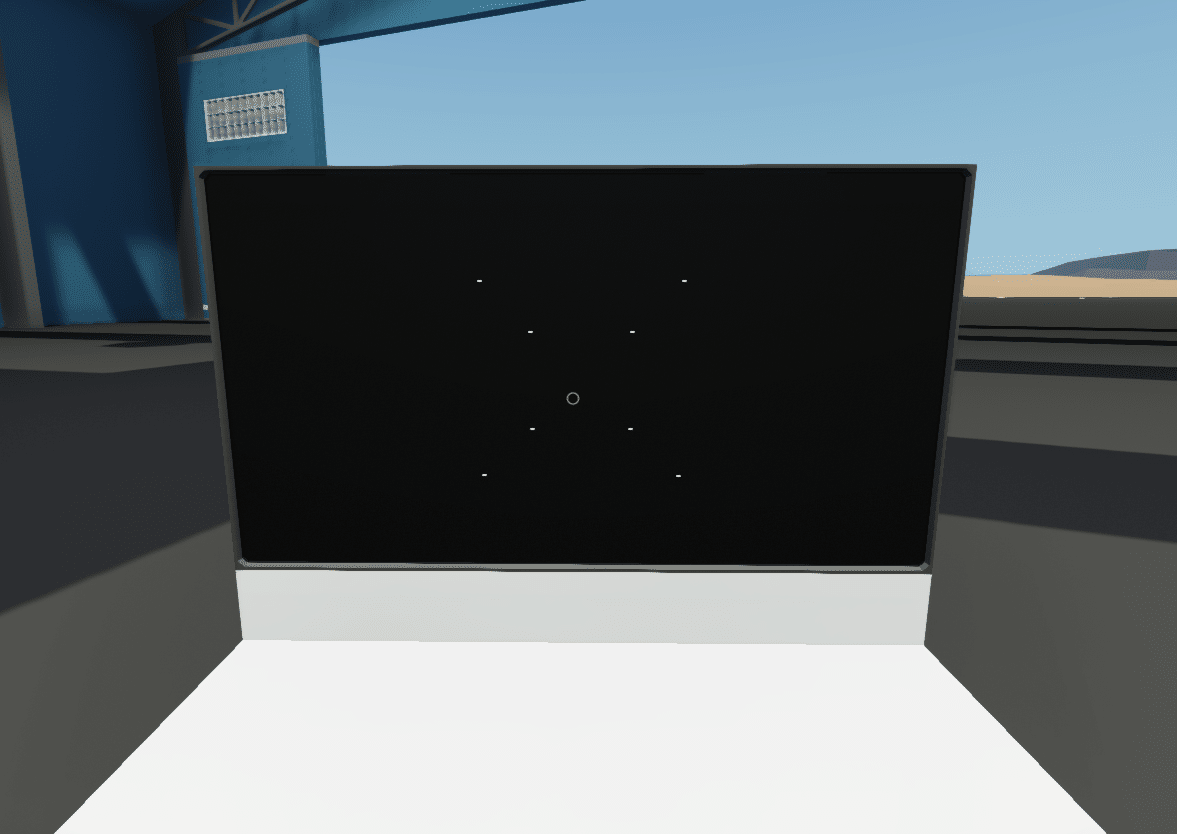
(3) 辺の描画
頂点が正しく描画されていたら、辺を描画してみましょう。ペアとなる頂点のモニター座標をそれぞれ求め、drawLine関数で2点間に線を引くことで辺が描画できます。コードは画像を参照。

(立方体を正面から見たところ)
これにてワイヤーフレーム完成!お疲れさまでした。
サンプルをワクショに上げておくので参考にしてね。
(Level 2)球体のワイヤーフレームを自動生成して回してみよう
さて、実際に手を動かしてワイヤーフレームを実装したわけですが、皆さんすでにお気づきかと思います。そう、頂点座標とペアの番号を手打ちで実装するのって超めんどくさいんですよ。
頂点数8、辺数12の立方体でも大変な作業なのに、より複雑な立体を描画するとなるともう人力ではどうしようもありません。そこで自動化です。退屈なことはLuaにやらせよう。
この章では、正12角形をベースにした頂点数62、辺数132の球体をワイヤーフレームで描画します。ついでに左右キーで球体を回転させられるようにしてみましょう。やっぱり3DCGは動かしてこそ楽しいですからね。
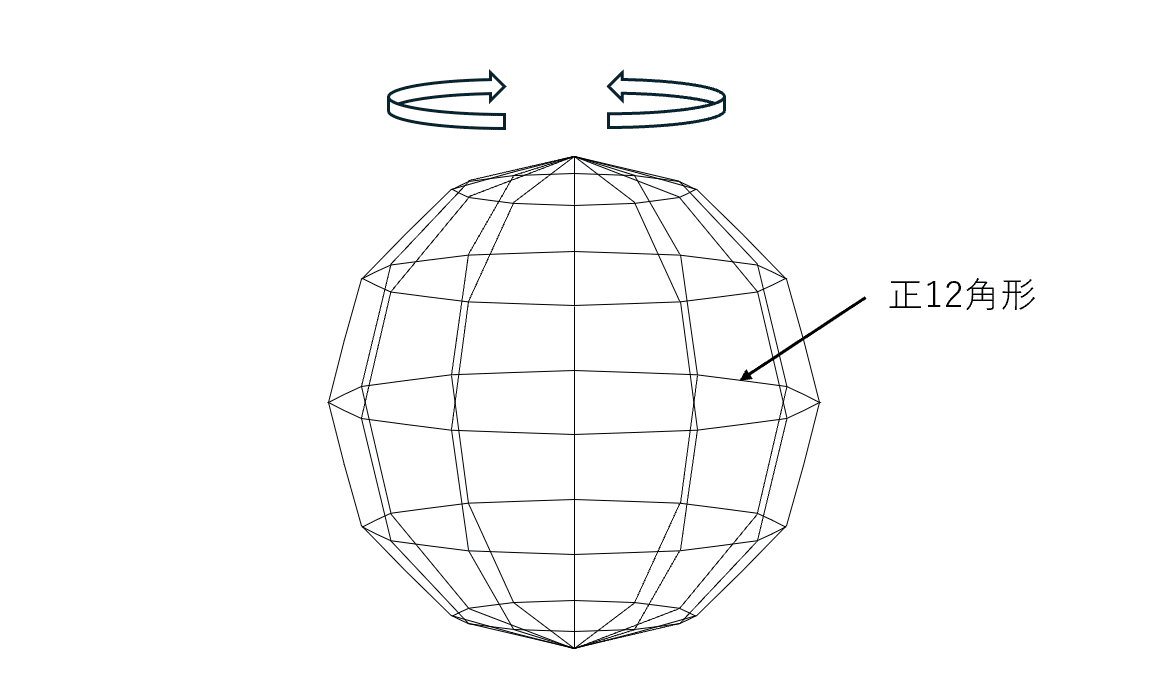
それでは、やっていきましょう。
(1) 頂点座標の決定
まず、各頂点に番号を振っていきます。今回はこんな感じ。
$${P_1=(0,-1,0), P_{62}=(0,1,0)}$$として、その間の点は図のように上から反時計回りに番号を振っていきます。
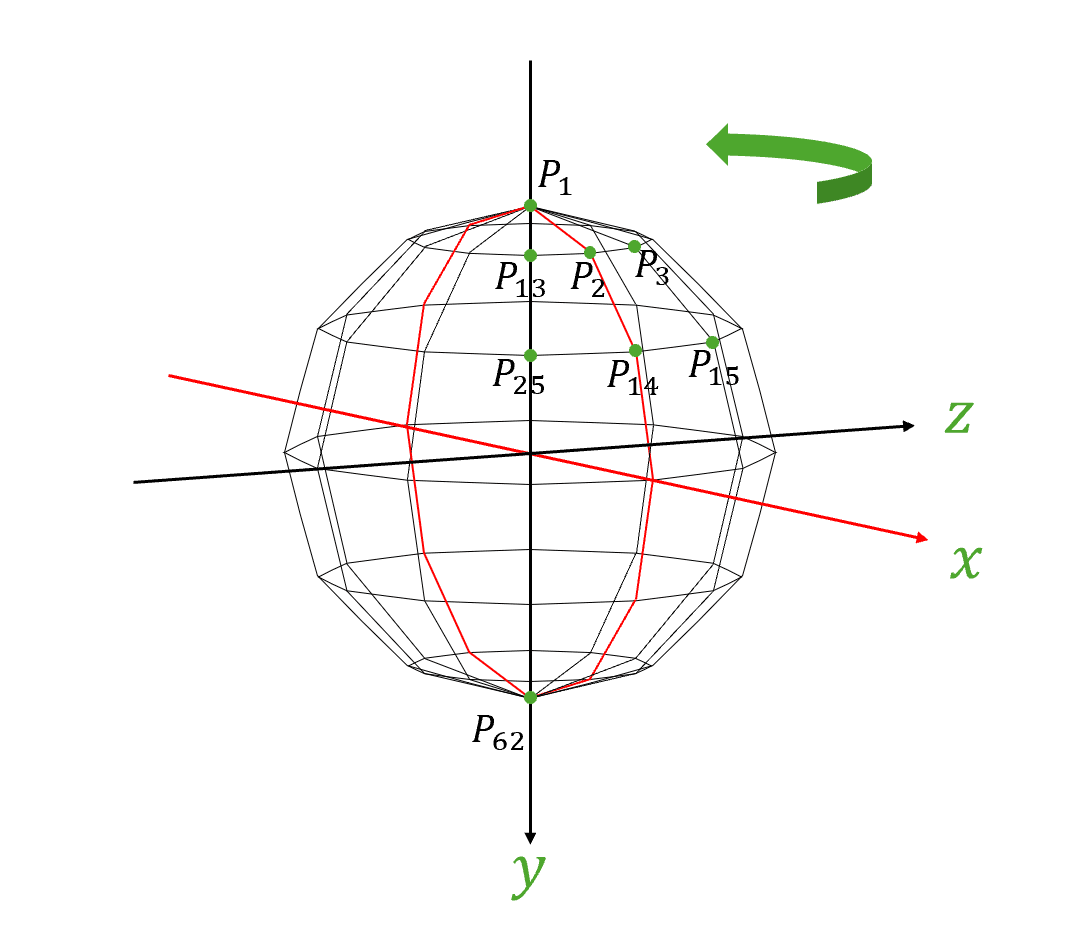
頂点座標を格納するテーブルにはこの順番でデータが入ることを覚えておいてくださいね。
さて、次は実際に座標を求めていきます。
まず、上から$${i}$$段目の正12角形上の点を、番号が若い順に1番目、2番目…と呼ぶことにしましょう。
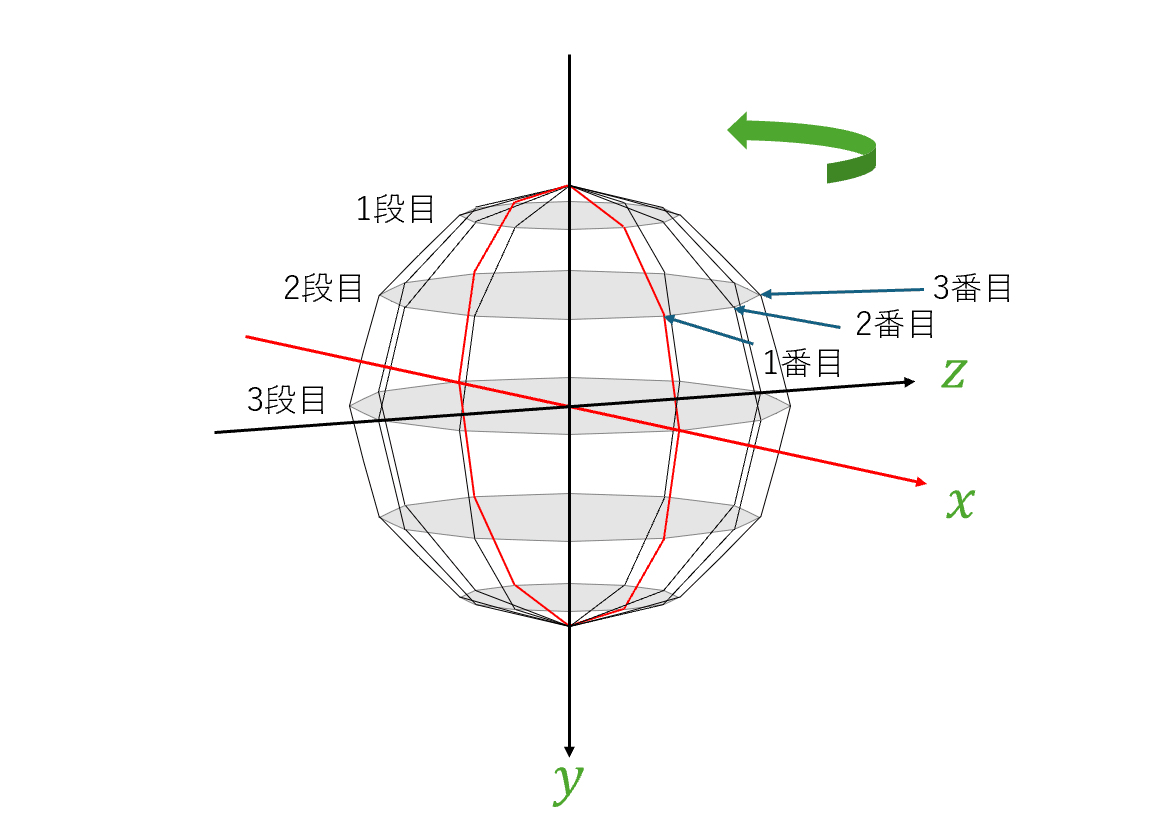
次に$${i}$$と$${j}$$を使って、$${i}$$段目$${j}$$番目の点の座標を表すことを考えます。
三角関数を使うよ!(数学苦手な人ごめん!)
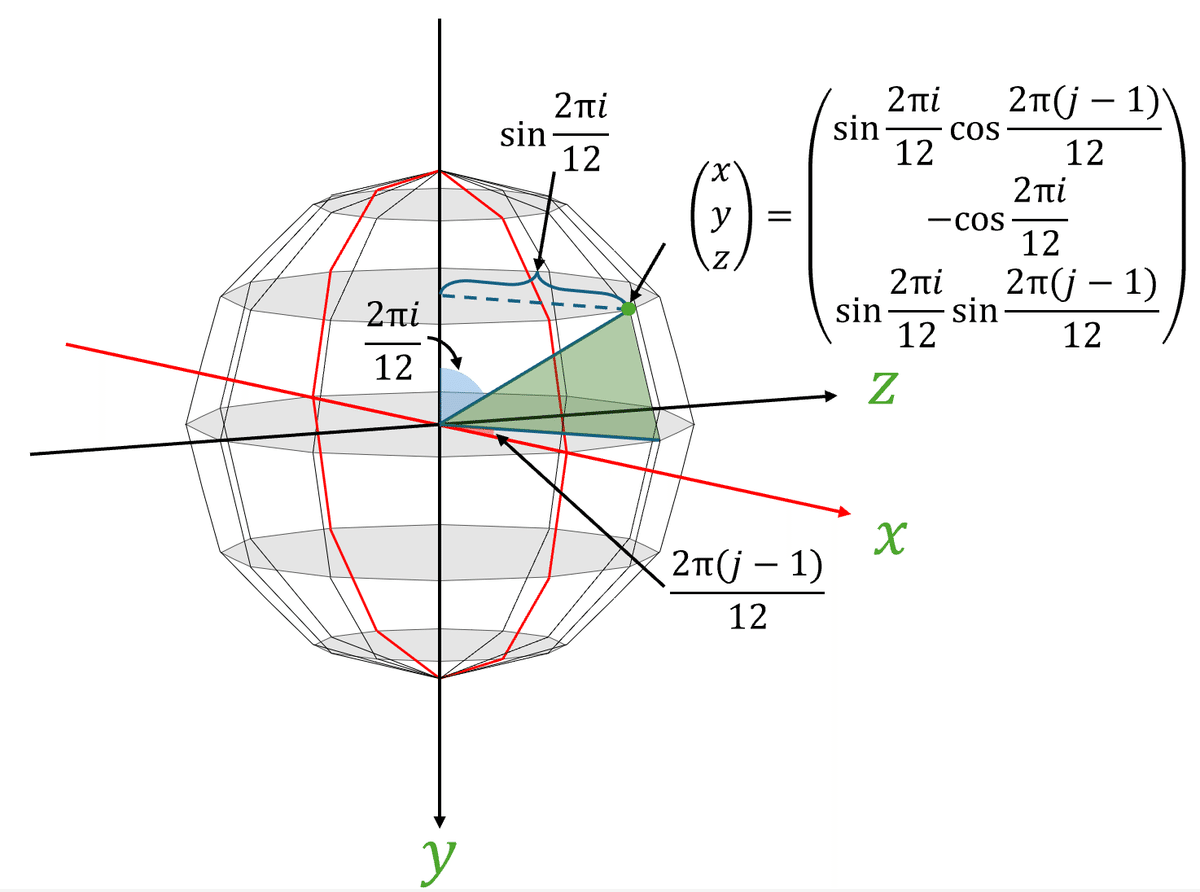
この図に示すとおり、$${i}$$段目$${j}$$番目の点の座標$${(x,y,z)}$$は、
$${(x,y,z)=(\mathrm{sin}\frac{2\pi i}{12}\mathrm{cos}\frac{2\pi (j-1)}{12}, -\mathrm{cos}\frac{2\pi i}{12}, \mathrm{sin}\frac{2\pi i}{12}\mathrm{sin}\frac{2\pi (j-1)}{12})}$$
と表すことができるんです。
これで終わりでもいいんですが、今回は左右キーで回転させたいのでもうひと工夫加えましょう。左右キーの入力に合わせて増減する回転角を$${\phi}$$とおくと、
$${(x,y,z)=(\mathrm{sin}\frac{2\pi i}{12}\mathrm{cos}(\frac{2\pi(j-1)}{12}+\phi), -\mathrm{cos}\frac{2\pi i}{12}, \mathrm{sin}\frac{2\pi i}{12}\mathrm{sin}(\frac{2\pi(j-1)}{12}+\phi))}$$
と書くことができます。(図の赤い角度に$${\phi}$$を足しただけだよ)
これで球体の頂点座標が回転するようになりました。やったね!
ちなみに、テーブルに座標を追加するときはtable.insert関数を使うと自動化できます。今後の必須テクなので覚えておきましょう。

(2) ペアとなる頂点番号の決定
ペアになる頂点番号を格納したテーブルも自動で作成されるようにしてみましょう。
まず、「何と何がペアになっているか?」を基準に、辺をこんな感じで4パターンに分類します。
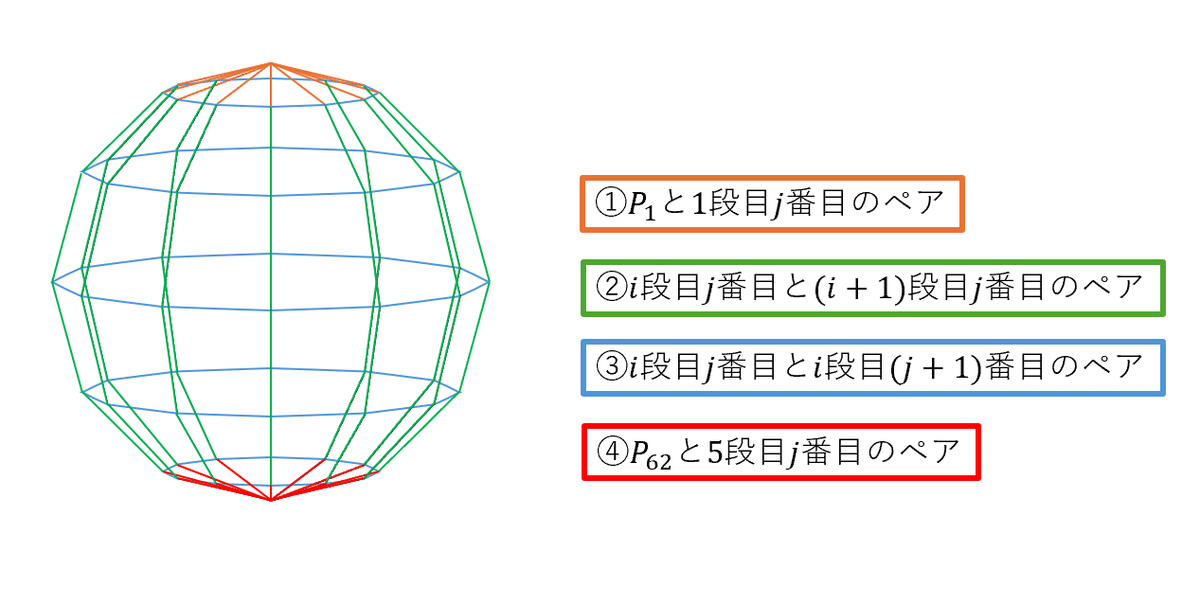
あとはこれに従って、for文をうまく使いながら辺を追加していきましょう。ここでもtable.insert関数が大活躍します。

(3) 実際に描画してみよう
描画についてはLevel1で作ったものがそのまま使えます!やったね。
実際に描画するとこんな感じ。
(表示が小さかったのでカメラの$${z}$$座標のみ$${z_c=-5}$$に変更)

こちらもサンプルをワクショに上げておきます。実装のヒントにしてみてくださいね。
(Level 3)ポリゴンを描画してみよう
さて次はいよいよポリゴンです!
皆さんポリゴンはご存知ですよね。種族値65-60-70-85-75-40、言わずと知れたポケモンショックの…え、それじゃない?

冗談はさておきポリゴンとは、3DCGで物体の面を表現するために使われる多角形(多くの場合三角形)およびそれを使った描画手法のことです。この技術を使うことで以前までは難しかった面や明るさの表現が可能となり、今までにないリアルな映像の描画が可能に。3DCGに革命をもたらしました。
さらに90年代半ばには初代プレステやセガサターン、Nintendo64が登場しポリゴン技術も広く普及。3Dゲーム時代が幕を開けることとなります。
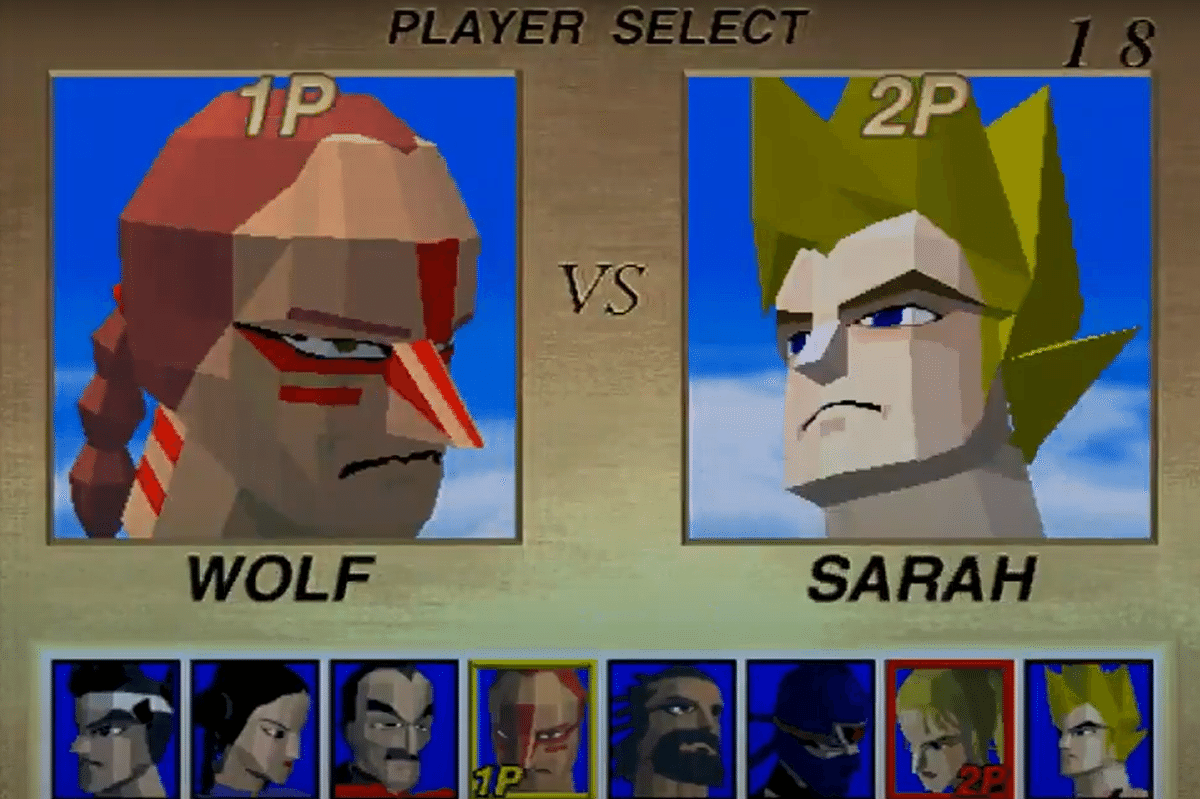
ポリゴン技術を全面的に使用した初期の名作
…とまぁ、背景だけ聞いていると何やら難しそうな感じがしますが、前章までの技術を習得した皆さんにとってはそこまで難しい技術ではないはずです!ポリゴン技術をマスターしてストワライフをもっと豊かにしよう。
(1) ポリゴンとワイヤーフレームの違い
ワイヤーフレームもポリゴンも、頂点を選んで線を引く(もしくは面を描く)技術。しかもストワのLuaにはありがたいことに、3頂点の座標を入力すると三角形を描いてくれるdrawTriangleF関数が存在します。
ってことはワイヤーフレームで2個1組だった頂点のペアを3個1組にして、drawLine関数の代わりにdrawTriangleF関数を使えば実装できそうですよね。
これ、方針は正しいんですが、実はこのままではうまくいきません。骨組みだけのワイヤーフレームは物体の裏側が見えても問題がないのに対し、面を張るポリゴンは裏側が見えてはいけないからです。これをなんとかしなくてはいけませんよね。

裏面が見えないよう工夫しないと表示が崩れてしまう
というわけで次項では、この問題の解決方法を紹介します。
(2) 内積を使った描画判定
最も簡単な方法として、ポリゴンの法線ベクトルと(ポリゴンから見た)カメラの方向ベクトルの内積を利用するものがあります。
各ポリゴンごとに法線ベクトルとカメラの方向ベクトルの内積を求め、値が正(法線とカメラのなす角が90°以内)ならポリゴンを描画し、負なら描画しない、という処理を行うわけです。
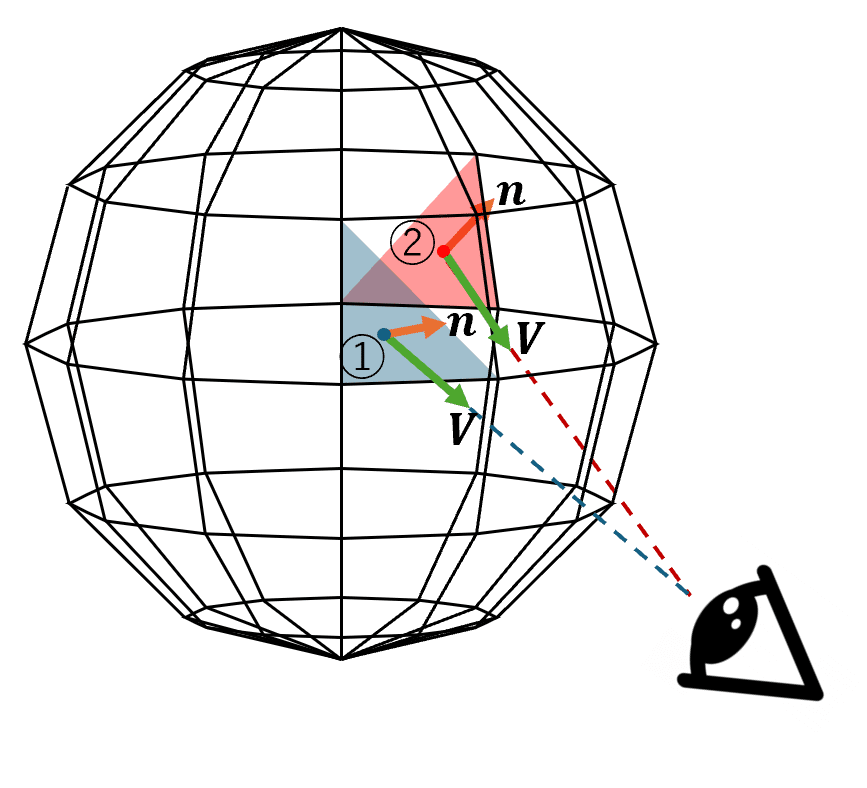
ベクトルについては今後、基本的に正規化して扱うよ
上の図の場合、ポリゴン①では$${\boldsymbol{n}\cdot\boldsymbol{V}>0}$$、ポリゴン②では$${\boldsymbol{n}\cdot\boldsymbol{V}<0}$$です。これを使ってポリゴンを描画するかどうかを判定することができるんですね。
( ^o^)これでポリゴンの問題は解決!
( ˘⊖˘) 。o(待てよ?ドーナツ形を横から見たときみたいに「法線はこっちを向いてるけど視点からは見えない面」があるとダメじゃないか?)
|ぺんぎんの家|┗(☋` )┓三
( ◠‿◠)☛気づいてしまったか… 残念だが消えてもらおう
▂▅▇█▓▒░(’ω’)░▒▓█▇▅▂うわああああああ
(気になった人は「ペインタアルゴリズム」「zバッファ法」あたりで検索。今回は球体しか描画しない&話がややこしくなるので扱わないよ)
(3) 実装!
それでは実装していきましょう!
まずはデータの格納方法から。Level2までは頂点を格納したテーブル(verts)と辺を格納したテーブル(edges)を使っていましたが、Level3からはedgesではなくポリゴン関連のデータを格納するテーブル(pols)を使うことにしましょう。
フォーマットはとりあえずこんな感じで行きます。(わかりやすさ重視の設計なので、慣れてきた人はもっと効率的なテーブル設計を試してもいいよ)
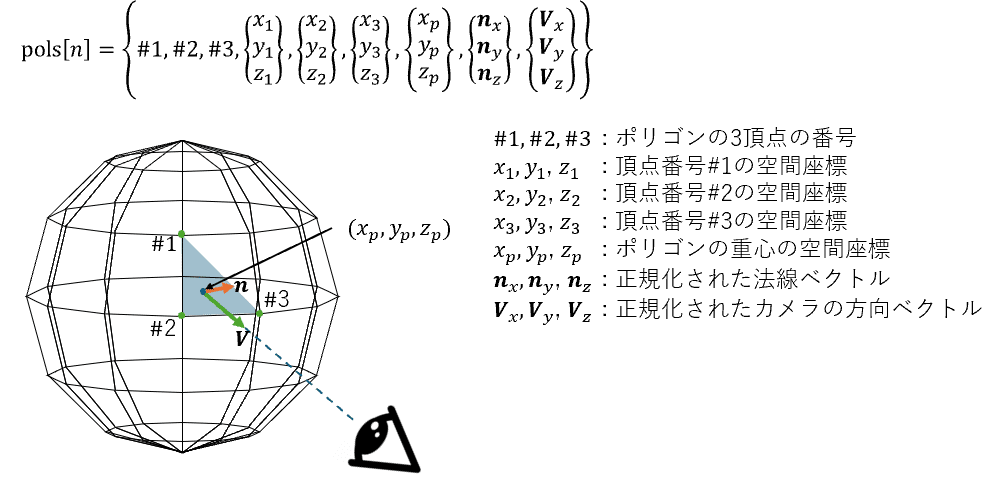
あとは実際にポリゴンを追加していくだけ。まず3頂点の番号を全ポリゴン分格納して、そのあとから残りのデータを追加するとスムーズです。
ポリゴンの追加は辺の時と同様、このように4パターンに分けて追加していきましょう。

今回の座標系の場合、ポリゴンの3つの頂点は表面からみて反時計回りの順番に追加するのを忘れないように注意。(順番が時計回りだと外積を取ったときに法線ベクトルの向きが逆になっちゃうよ)

ポリゴンの頂点番号が追加出来たら残りのデータを埋めていきましょう。
法線ベクトルは外積を使って求めることができます。(正規化を忘れずにね)
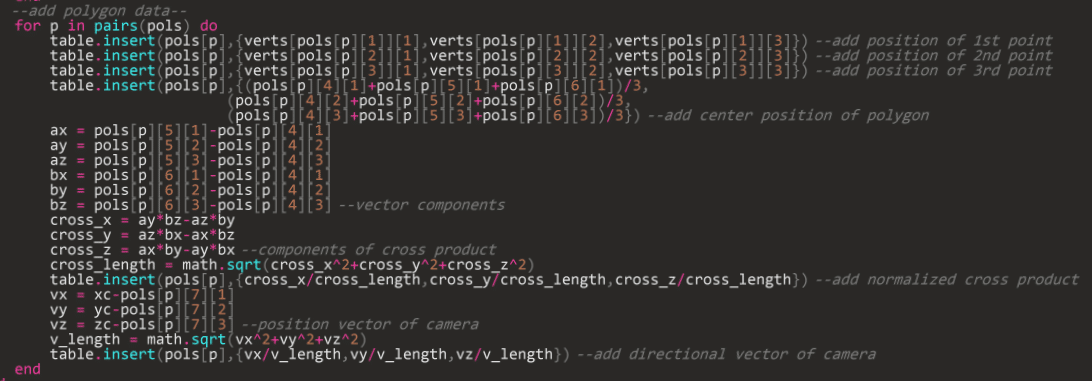
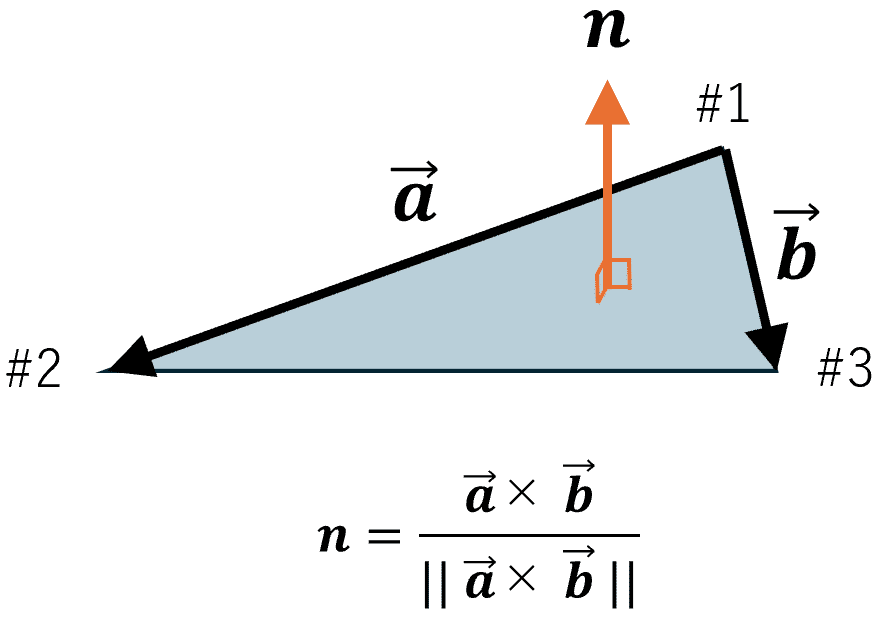
(4) 描画してみよう
テーブルができたらdrawTriangleF関数を使って描画してみましょう。
さぁ、結果がこれだ!

なんか白い丸が出てきました。
これのどこが3Dなんだ!と言いたくなるところですが、現在の設定ではポリゴンをすべて同じ色で描画しているので当たり前といえば当たり前ですね。ちゃんと3Dで描画できているか確かめるために、ポリゴン番号が奇数の時と偶数の時で色を分けてみましょう。


ちゃんと3Dポリゴンが描画されていました。やったー!
(もちろん左右キーで回せるよ)
これにて長かったポリゴン編も終了。お疲れさまでした。
ワクショにサンプルも上げておくのでわからないところがあったら参考にしてね。
(Level 4)ライティングを実装しよう
さて、苦労して実装したぶん感動もひとしおだったポリゴン描画ですが、見慣れてくるとなんかちょっと物足りない感じがしませんか?

そう、3DCGなのに陰影がないせいで立体感が失われ、のっぺりして見えてしまうんです。
本章ではさらなるリアリティを求める皆さんのために、光源処理(ライティング)の実装テクニックを学んでいきます。
なんだか難しそうなイメージを持たれているかもしれませんが大丈夫!ここまでついてこられた皆さんなら難なく理解できるはず。光源処理をマスターして凄腕ワーカーになろう。
(1)光源処理(ライティング)ってなーに?
そもそも、3DCGにおける光源処理ってどうやって行われているんでしょうか?
ざっくり言ってしまえば、ポリゴンの色を変えているだけです。光が当たっているところは明るい色で、影になっているところは暗い色でポリゴンを描写してあげることで、現実世界のものの見え方を模しているわけですね。
ポリゴンの色の求め方にはたくさんの種類があるんですが、今回はその中でも最も簡単かつ広く使われているPhongの反射モデルを使っていきます。
(2) Phongの反射モデル
Phongの反射モデルは、光が当たった時のポリゴンの色を
・Ambient項 : シーン全体を照らす光による反射 (全体が均一に明るくなる)
・Diffuse項 : 光源からの光の拡散反射 (光源に照らされた部分が明るくなる)
・Specular項 : 光源からの光の鏡面反射 (光源が物体に反射して明るくなる)
の3つに分類して処理するモデルです。

数式で表すと下の図のようになります。
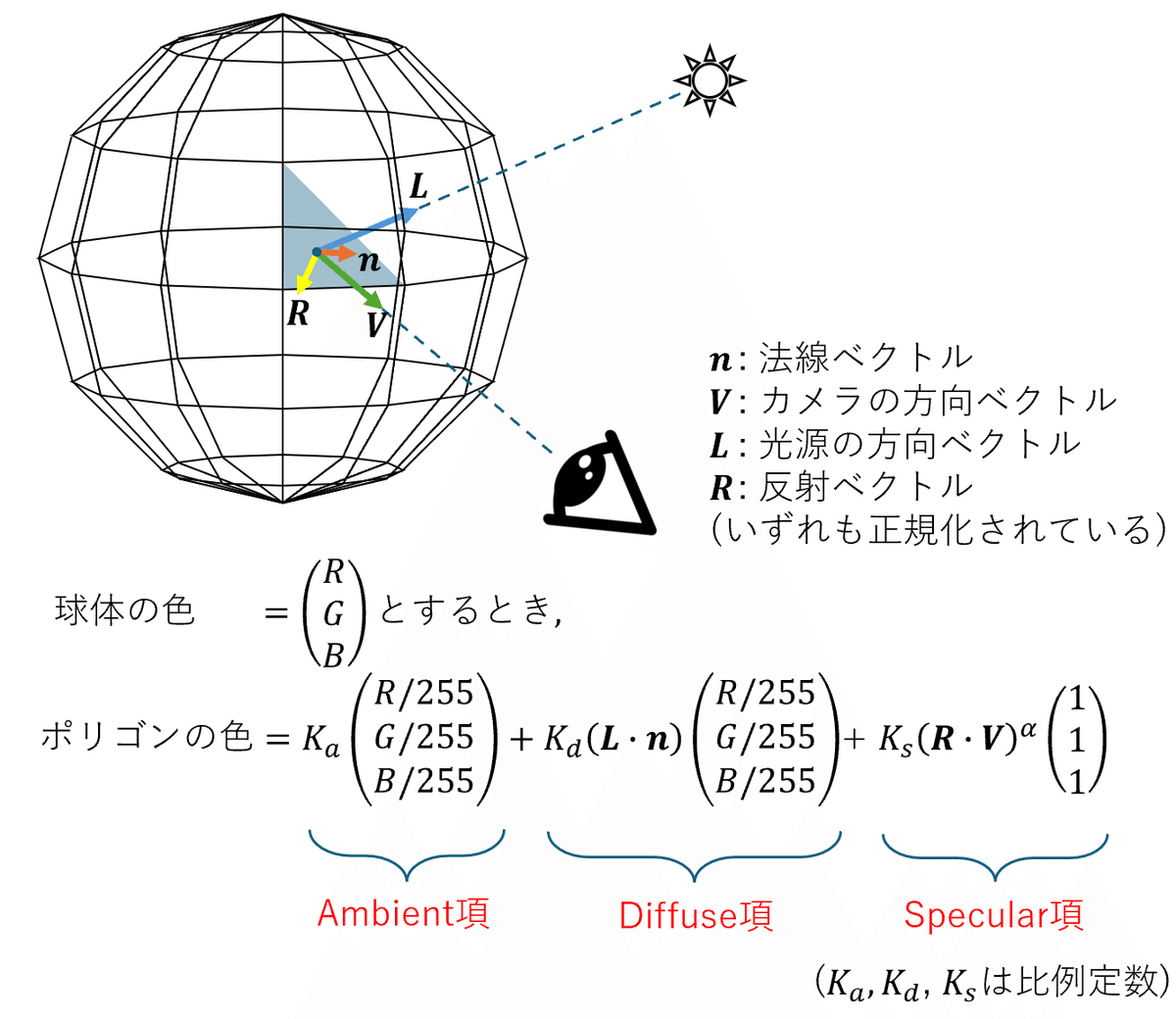
ここで大事なのは、
・Ambient項は物体全体で一定
・Diffuse項は光源の方向ベクトルと法線ベクトルの内積に比例
・Specular項は反射ベクトルとカメラの方向ベクトルの内積の定数乗に比例
ということ。これを覚えておきましょう。
今回は$${K_a=10,K_d=100,K_s=100,\alpha=10}$$とします。
(3) 実装!
それでは実装していきましょう!
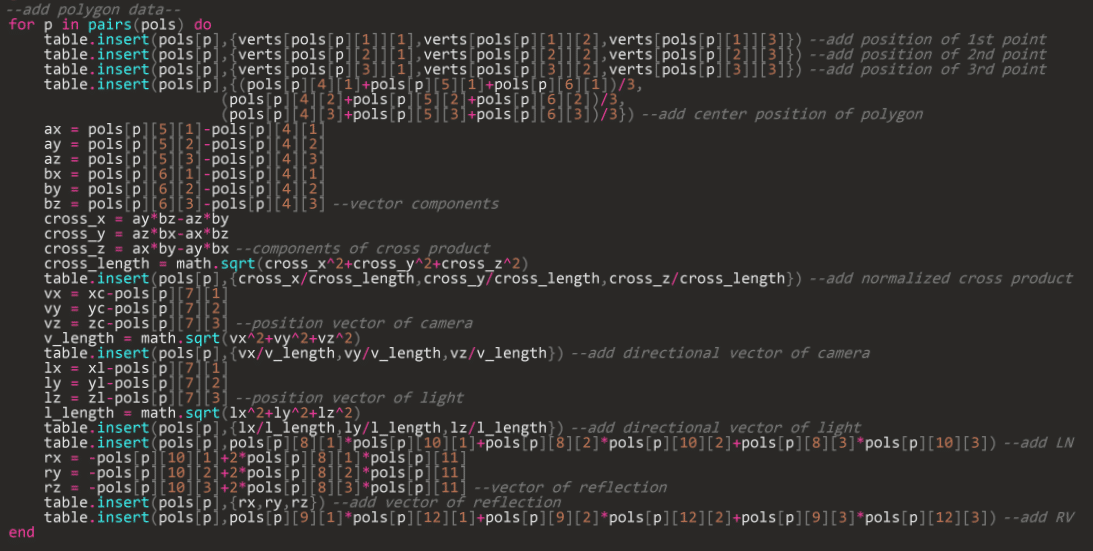
まずはデータの追加から。Level3で作ったpolsに新たなデータを格納していきます。
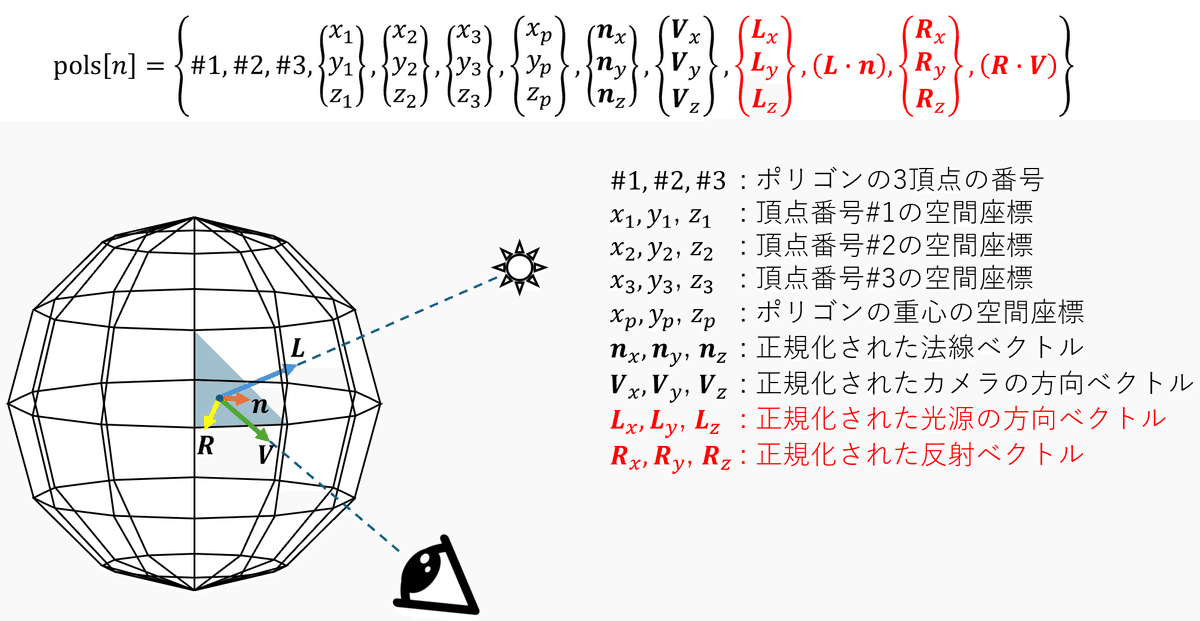
$${\textbf{\textit{R}}}$$はこんなふうに求められます。参考までに。
$${\textbf{\textit{R}}=-\textbf{\textit{L}}+2(\textbf{\textit{L}}\cdot\textbf{\textit{n}})\textbf{\textit{n}}}$$
(3) 描画してみよう
テーブルが出来上がったので実際に描画してみましょう。
今回は光源の位置を$${(3,-3,-5)}$$,球体の色を$${(255,0,255)}$$、球の分割数を$${n=48}$$とし、screen.setColor関数でPhongの反射モデルを実装して動かしてみます。結果がこれだ!

なんか左下のほうがバグってしまいました。
これはscreen.setColor関数に負の値を入力すると値がアンダーフローして誤動作するためです。これを防ぐために負の値は0として扱うようにしましょう。
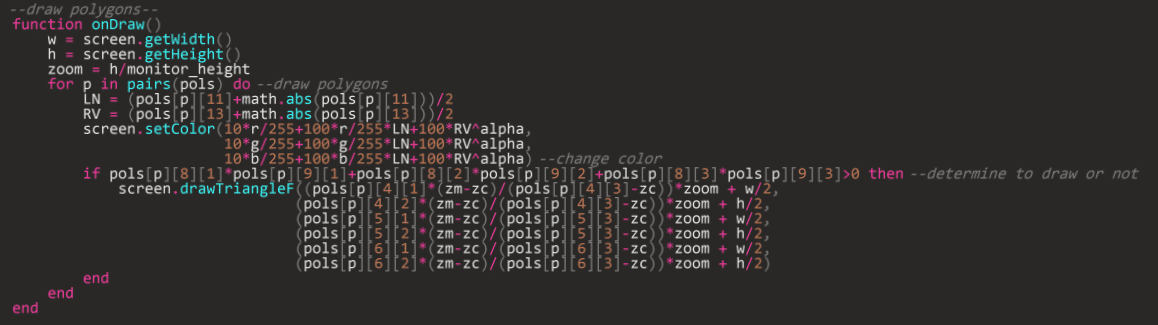
LNとRVが負の値なら0となるよう、
$${LN=(\textbf{\textit{L}}\cdot\textbf{\textit{n}}+|\textbf{\textit{L}}\cdot\textbf{\textit{n}}|)/2}$$
$${RV=(\textbf{\textit{R}}\cdot\textbf{\textit{V}}+|\textbf{\textit{R}}\cdot\textbf{\textit{V}}|)/2}$$
としています。
これを実行したものがこちら。
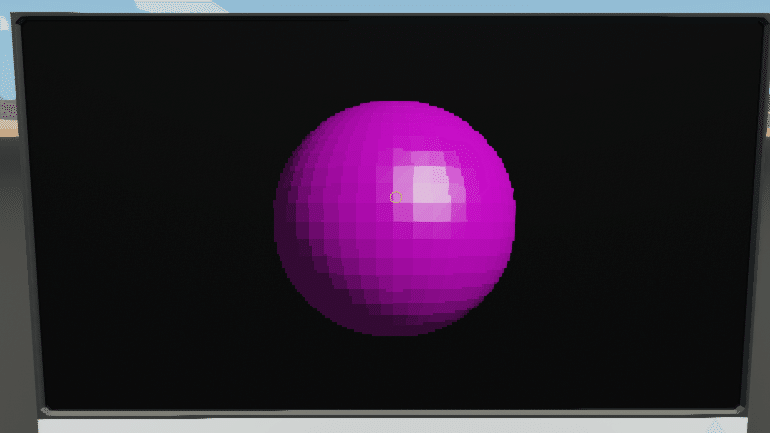
これにて最終レベル、Level4完結です。本当にお疲れ様でした!
例によってサンプルをワクショに上げておきます。参考にどうぞ。
(ワクショ版は負荷軽減のため分割数を$${n=24}$$にしてあるよ)
おわりに

「Stormworksで学ぶ!3DCG入門」は以上となります。
正直、シェーディング補間やテクスチャマッピング、レイトレーシング等語りたいことはまだまだあるのですが、ストワのLuaでやるには負荷が高い&ここまで辿りついた皆様なら独力で習得できると思い、泣く泣くカットしました。(好評だったら続編でやるかも?)
スポーンさせてからビークル上で3Dモデリングができるよ
今回初めて解説記事を書いてみましたが、わからない部分があったら遠慮なくTwitter(@ursaminor_alpha)まで連絡ください。
それから、「自分でも3DCG作ってみたよ」って人がいれば連絡してくれると泣いて喜びます。
最後まで読んでくれてありがとう。ぜひ皆さんも自分で作って、ストワ3DCGの奥深さを体験してみてくださいね!
(おわり)
