Python を用いての 効率的フロンティア と ポートフォリオの最適化 Efficient Frontier & Portfolio Optimization with Python [Part 2/2]

ーーーーーーーーーーー2021/07/28　追記ーーーーーーーーーーー
Pythonの一部仕様変更などでうまく動いていなかった部分を新しいサイトでは修正しました。

今後適宜修正や改修を行おうとは思いますが、すべてを改修できるわけではないことはご承知おきください。

2021/07/28時点では動いていることは確認しております。

今後こちらに移行します。

Python を用いての 効率的フロンティア と ポートフォリオの最適化 Efficient Frontier & Portfolio Optimization with Python [Part 2/2]

ーーーーーーーーーーー2021/07/28　追記ーーーーーーーーーーー

実際のPythonコードを示しての効率的フロンティア と ポートフォリオの最適化を行う記事になります。

元ネタは以下の英文記事になります。

Efficient Frontier & Portfolio Optimization with Python [Part 2/2]

この記事の対象とするユーザー

・効率的フロンティア　（Efficient Frontier）について知識がある、もしくは興味を持っている方
・米国株のポートフォリオ運用に効率的フロンティア　（Efficient Frontier）の考え方を用いて、最適化、リターンの向上並びにリスクの低減を考えている方
・解析を行うPythonプログラムコードに興味のある人

基本的にはコードをコピペすれば動くことを確認していますが、理論の内容の理解や、プログラムの理解などあった方がより深く理解できると思います。

この記事で使用するもの

・Google ColaboratoryのPython

となります。

上記の記事ではQUANDLというデータ配信サービスを使用してのデータ取得となっているので、それを
・Yahoo USからのデータ取得
・Google ColaboratoryのPythonを使う
ことにより、無料で、簡単に行おうということになります。

Quandl

Quandlとは

QuandlはNasdaq傘下のでーは配信サービスプロバイダーになります。

Nasdaq Acquires Quandl to Advance the Use of Alternative Data

私もアカウントを持っていて、利用させていただいてます。
APIを利用して高品質なデータを配信しており、株価のヒストリカルデータだけでなくPBR,PERといったファンダメンタルデータなども提供しています。

API接続について

IB証券（インタラクティブ・ブローカーズ証券 ）でもAPIによるデータアクセスは可能ですが、アクセススピードや簡便な操作方法など、頻繁にデータアクセスを必要する方は、Quandlはサービス契約を検討すべき・検討に値するサービスを提供しています。

IB証券（インタラクティブ・ブローカーズ証券 ）のヒストリカルデータへのAPI接続については以前書いた以下の記事を参考にしてください。

効率的フロンティア　（Efficient Frontier）とは

効率的フロンティアについてだけで、非常に多くの記事があるくらい奥深いものですので、ここでは概略だけ取り扱います。

みずほ証券が紹介している「ファイナンス用語集」のリンクを紹介します。

効率的フロンティア | みずほ証券 ファイナンス用語集

効率的フロンティア　（Efficient Frontier）とは、分散投資を実施したときに実現するポートフォリオの中で、あるリスクの水準で最大のリターンを獲得できるポートフォリオの集合のこと

また、オリジナルの英文記事にも説明があります。

Markowitz’s Efficient Frontier in Python [Part 1/2]

数学的なバックグラウンドに興味のある方は以下のサイトなども使って勉強すると良いと思います。

現代ポートフォリオ理論 - Wikipedia

Google Colaboratoryのpythonでの利用方法

以下の記事を読んで、Google Colaboratoryを利用できるようにしておいてください。

実際のコード前半は以下のようになります。

# import needed modules
import datetime
import fix_yahoo_finance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
start = datetime.date(2018,1,1)
end = datetime.date.today()

# get adjusted closing prices of 5 selected companies with Quandl
selected = ['CNP', 'F', 'WMT', 'GE', 'TSLA']
data = yf.download(selected, start=start, end=end)["Adj Close"]

# calculate daily and annual returns of the stocks
#returns_daily = table.pct_change()
returns_daily = data.pct_change()
returns_annual = returns_daily.mean() * 250

# get daily and covariance of returns of the stock
cov_daily = returns_daily.cov()
cov_annual = cov_daily * 250

# empty lists to store returns, volatility and weights of imiginary portfolios
port_returns = []
port_volatility = []
sharpe_ratio = []
stock_weights = []

# set the number of combinations for imaginary portfolios
num_assets = len(selected)
num_portfolios = 50000

#set random seed for reproduction's sake
np.random.seed(101)

# populate the empty lists with each portfolios returns,risk and weights
for single_portfolio in range(num_portfolios):
   weights = np.random.random(num_assets)
   weights /= np.sum(weights)
   returns = np.dot(weights, returns_annual)
   volatility = np.sqrt(np.dot(weights.T, np.dot(cov_annual, weights)))
   sharpe = returns / volatility
   sharpe_ratio.append(sharpe)
   port_returns.append(returns)
   port_volatility.append(volatility)
   stock_weights.append(weights)
   
# a dictionary for Returns and Risk values of each portfolio
portfolio = {'Returns': port_returns,
            'Volatility': port_volatility,
            'Sharpe Ratio': sharpe_ratio}
            
# extend original dictionary to accomodate each ticker and weight in the portfolio
for counter,symbol in enumerate(selected):
   portfolio[symbol+' Weight'] = [Weight[counter] for Weight in stock_weights]

# make a nice dataframe of the extended dictionary
df = pd.DataFrame(portfolio)

# get better labels for desired arrangement of columns
column_order = ['Returns', 'Volatility', 'Sharpe Ratio'] + [stock+' Weight' for stock in selected]

# reorder dataframe columns
df = df[column_order]

# plot frontier, max sharpe & min Volatility values with a scatterplot
plt.style.use('seaborn-dark')
df.plot.scatter(x='Volatility', y='Returns', c='Sharpe Ratio',
               cmap='RdYlGn', edgecolors='black', figsize=(10, 8), grid=True)
plt.xlabel('Volatility (Std. Deviation)')
plt.ylabel('Expected Returns')
plt.title('Efficient Frontier')
plt.show()

Quandlのデータ取得の代わりにYahooUSからデータを取得します。
また、今回はデータの取得期間を2018年1月1日から現在の日付までとしています。
また、取得する銘柄はオリジナルのコードと同じ
['CNP', 'F', 'WMT', 'GE', 'TSLA']
といった銘柄群としました。

この辺りは使用する人によって銘柄を増やしたり、減らしたり、ETFで行ったり、工夫ができる部分だと思います。

import datetime
import fix_yahoo_finance as yf

start = datetime.date(2018,1,1)
end = datetime.date.today()

selected = ['CNP', 'F', 'WMT', 'GE', 'TSLA']

data = yf.download(selected, start=start, end=end)["Adj Close"]

そのような部分を行っているのが上記の部分になります。

次のパートでは価格の変化をパーセントでの表記に換え、それを年率換算に換えています。

# calculate daily and annual returns of the stocks
#returns_daily = table.pct_change()
returns_daily = data.pct_change()
returns_annual = returns_daily.mean() * 250

株価のパーセント騰落率の共分散「Covariance」を求め、それも年率換算値を求めます。

# get daily and covariance of returns of the stock
cov_daily = returns_daily.cov()
cov_annual = cov_daily * 250

その後の部分はそれぞれ異なったウェイトでの50,000個のポートフォリオを作ります。ウェイトが異なるのでリターンとボラティリティもポートフォリオごとに異なります。

投資家のリターンとリスクの比を表す指標のうちの一つ、シャープレシオで色付けすると以下のようになりなります。

ノーベル賞を取ったマーコウィッツの資本資産価格モデルCapital Asset Pricing Model (CAPM)で見慣れたグラフが出てきます。

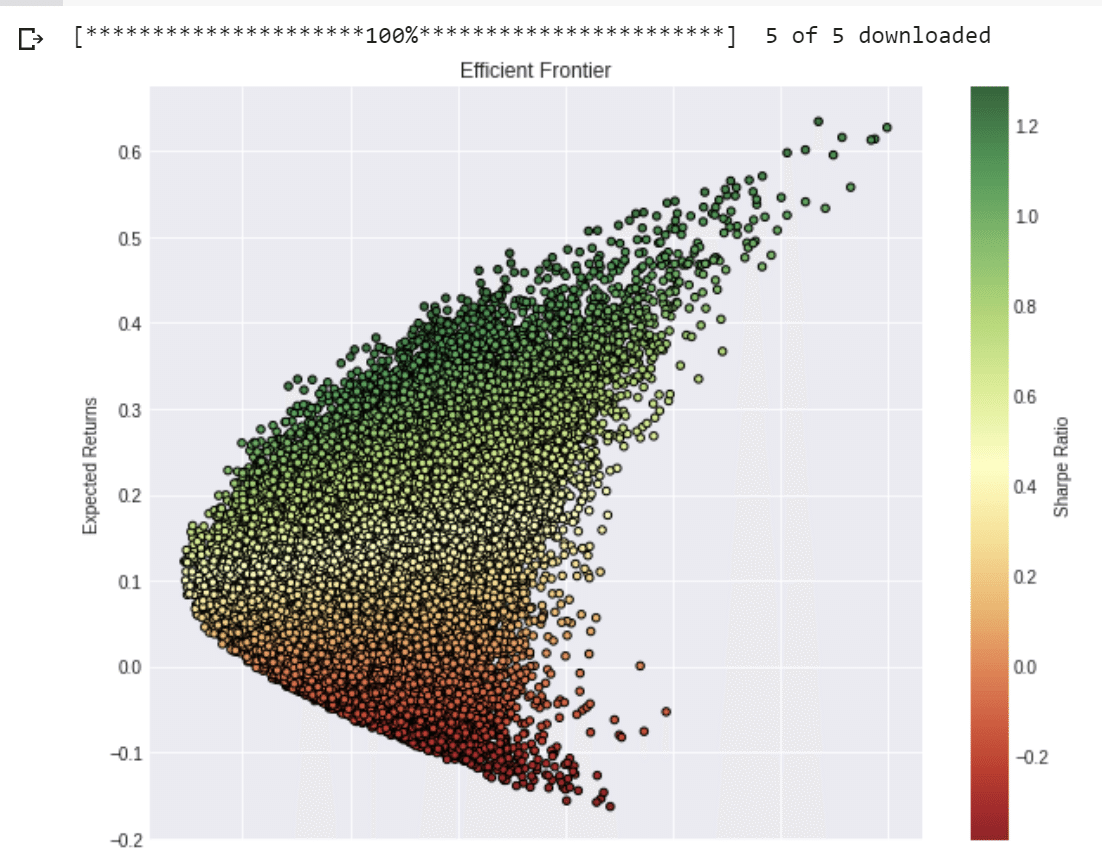
# find min Volatility & max sharpe values in the dataframe (df)
min_volatility = df['Volatility'].min()
max_sharpe = df['Sharpe Ratio'].max()

# use the min, max values to locate and create the two special portfolios
sharpe_portfolio = df.loc[df['Sharpe Ratio'] == max_sharpe]
min_variance_port = df.loc[df['Volatility'] == min_volatility]

# plot frontier, max sharpe & min Volatility values with a scatterplot
plt.style.use('seaborn-dark')
df.plot.scatter(x='Volatility', y='Returns', c='Sharpe Ratio',
               cmap='RdYlGn', edgecolors='black', figsize=(10, 8), grid=True)
plt.scatter(x=sharpe_portfolio['Volatility'], y=sharpe_portfolio['Returns'], c='red', marker='D', s=200)
plt.scatter(x=min_variance_port['Volatility'], y=min_variance_port['Returns'], c='blue', marker='D', s=200 )
plt.xlabel('Volatility (Std. Deviation)')
plt.ylabel('Expected Returns')
plt.title('Efficient Frontier')
plt.show()

後はボラティリティが最小になる点とシャープレシオが最大になる点を探してプロットすると以下のようになります。

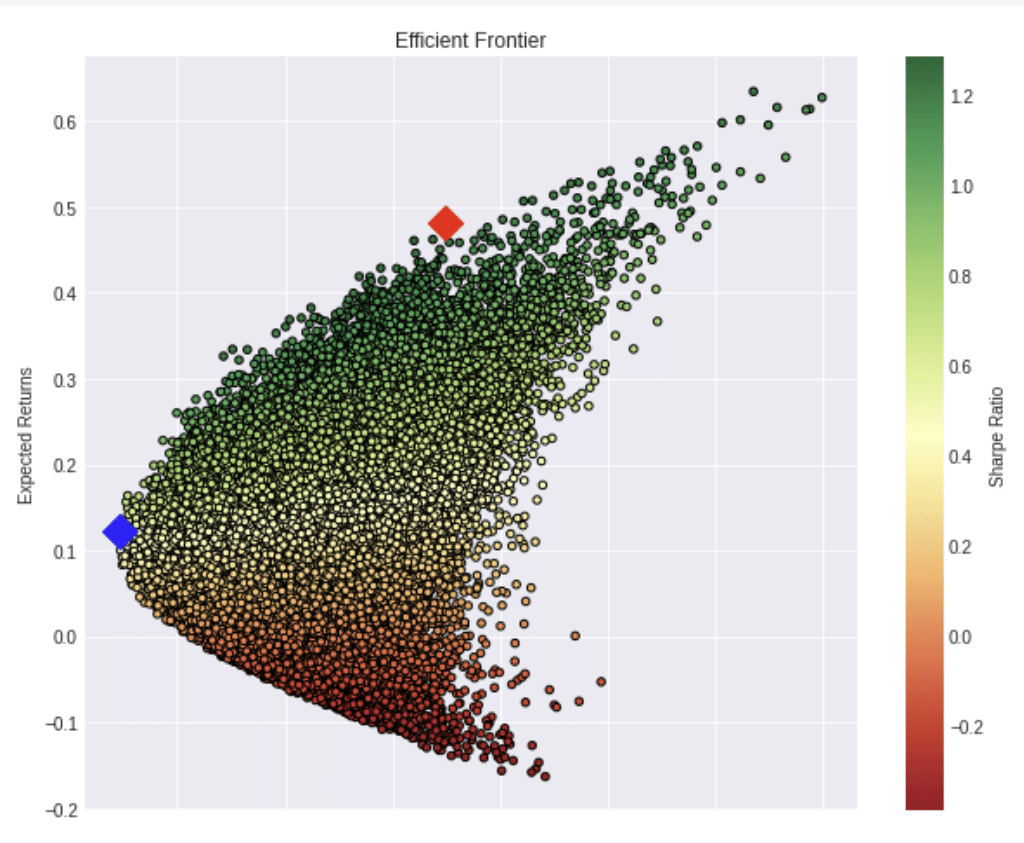
青い点がボラティリティが最小となるポートフォリオで、赤がシャープレシオが最大になるものです。それぞれ、どの銘柄がポートフォリオにおいて、どのくらいのウェイトを占めるのかを表示すると以下のようになります。

# print the details of the 2 special portfolios
print(min_variance_port.T)
print(sharpe_portfolio.T)

34461
Returns 0.122298
Volatility 0.222989
Sharpe Ratio 0.548451
CNP Weight 0.064623
F Weight 0.172365
WMT Weight 0.020066
GE Weight 0.035020
TSLA Weight 0.707926
29859
Returns 0.481098
Volatility 0.374205
Sharpe Ratio 1.285653
CNP Weight 0.050388
F Weight 0.004180
WMT Weight 0.000638
GE Weight 0.501385
TSLA Weight 0.443409

今回の例ではこのような数字になりました。
ボラティリティを抑えて、代わりにリターンを犠牲にするタイプのポートフォリオの割にはTSLAが大きめに見えたり、シャープレシオが最大にするためにはGEとTSLAの実質2銘柄でいいとか、、いろいろ先入観とは違うような結果も出てきそうです。

今回は2018年以降のデータを使っていること、使用した銘柄数もオリジナルのページのものを使っていますので、個人的にいろいろ変更して、使ってみるのもよいかと思います。

投資に関する免責事項
プログラムや考え方の情報の提供・作業代行を目的としており、投資勧誘を目的とするものではありません。

過去のデータを用いた解析は、将来の株価の推移を保証するものではないことをはご承知おきください。

また、どのような銘柄を選定するか、等ウェイトではどうなのかといった、ウェイトの掛け方等、さらなるブラッシュアップが可能であると思います。

役に立ったと思いましたらこの記事の「いいね」をよろしくお願いします。

ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー

Pythonで資産運用モデルを作成する記事をまとめました。
Pythonを用いて、株価取得、チャート表示、株価分析、可視化、株価予測、株価の機械学習、ポートフォリオの構築、ポートフォリオの最適化、スクレイピングなどを行う記事を集めました。
もし興味を持っていただけるなら読んでみてください。

Pythonで資産運用モデル作成｜TF｜note