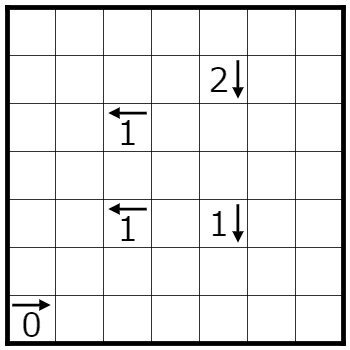
Castle Wall についてできるだけ真面目に考えてみた結果

　はじめに

　遅れて本当に申し訳ございません！　こちらはペンシルパズル Advent Calendar 2020の記事になります。

　皆さんはじめまして。ネオンです。
　よく Puzzle Square JPというサイトでペンシルパズルを投稿させてもらっています。
　まだ一年半ほどしか触れられていませんが、たまたま見かけたので勢いで参加しました。

　さて、今回はタイトルにもある通り、Castle Wall について話していきたいと思います。（？）

　Castle Wallとは？

　一応、Castle Wall について手短に説明します。もう分かっているよ、という方は飛ばしてもらっても構いません。

　Castle Wall は、2009年に Palmer Mebane 氏によって作られたループ系のペンシルパズルです。彼のブログサイトである Melon's Puzzles というサイトにて初めてルールと例題が掲載されました。

　分かりやすく日本語に訳したルールは以下になります。（Puzzle Square JPより）

　1. 盤面のいくつかのマスに線を引いて、全体で１つのループを作ります。
　2. 線はマスの中央を通るようにタテヨコに引きます。線を交差させたり、枝分かれさせたりしてはいけません。
　3. 枠線で囲まれた白マスと黒マスに線を引いてはいけません。
　4. 数字は、矢印の方向に伸びている直線の長さの合計を示します。
　5. 枠線で囲まれた白マスはループの内側に、黒いマスはループの外側になります。

　ここで面白いと思ったのが、黒マスと白マスの存在についてです。しかしその前に、本数定理について触れてみましょう。

　本数定理について

　皆さんは本数定理のことはご存知だと思います。偶端、端偶法などと言ったりすることもありますが、枝分かれのないループを使ったパズルにおいて、どの領域に注目しても線は必ず偶数本入る、ということです。
　例えば下の図で、×の部分から線が入ってしまうと、どうやっても一本余ってしまうので、入れないという感じです。

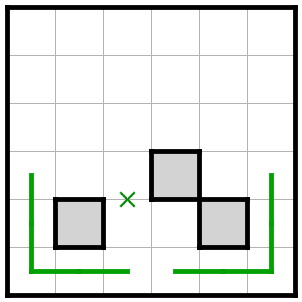
　非常に便利で、手筋の応用にも利く本数定理ですが、いくつかデメリットがあると考えています。

　その1：線が多いと、数えるときに間違えやすい（面倒くさい）

　これは、パズルが大きいほど発生しやすいです。
　簡易なアンケートを行ってみたところ、およそ80％が「ある」と回答しています。

　その2：知覚的に認知するのが難しい（見づらい）

　あまり慣れていなかったうちは、ここで本数定理が使える！　と気づけなかったり、場面から少し目を離すとこんがらかったりしました。

　ということで、本数定理を少し発展させた、境界定理（仮）というものを考えてみました。内容については以下の通りです。

　境界定理（仮）

　ここで Castle Wall に出てきた黒マスと白マスの概念を使います。

　・枝分かれや交差のない1つのループにおいて、内側にあるマスを白マス、外側にあるものを黒マスとする。
　・このとき、2マスが異なる色（白黒、黒白）ならその間を奇数本、同じ色（白白、黒黒）なら間を偶数本通る。これは逆についても言える。

　やんわりとした証明

とりあえず、2マスの間に n本の線が通る状態を命題 A(n) と定義します。

そして、下の図について考えます。

マスの定義から、黒マスと白マスの間には必ず線が通るので、1本引けます。

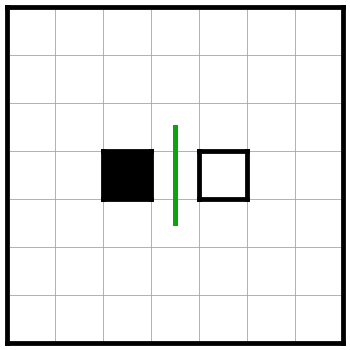
なので、A(1) の場合、2マスの色は異なるということが分かります。

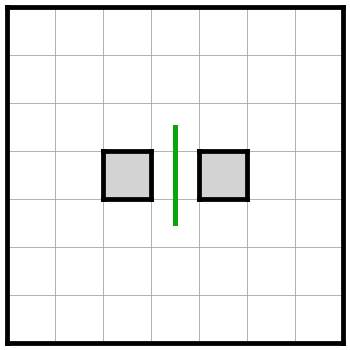
今度は A(2) について考えてみます。

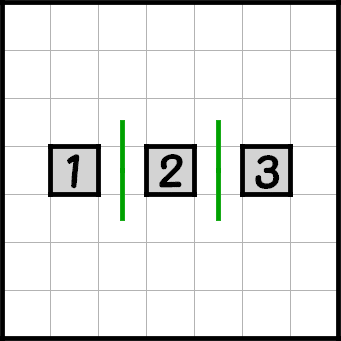
A(1) より、1と2の色、そして2と3の色は異なることが分かります。また、色は黒と白のみなので、1と3の色は同じですね。

なので、 A(2) の場合は2マスの色は同じということが分かります。

最後に一般化して、A(n) と A(n+1) の関係性に注目してみましょう。

図のように、A(n+1) は A(n) と A(1) に分けることが出来ます。

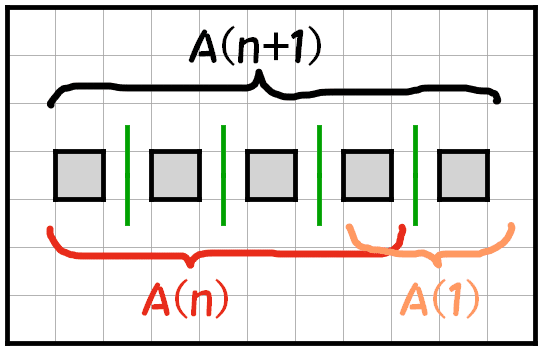
このことから、命題 A(n+1) は命題 A(n) の裏であることが分かります。

したがって、以下の命題は真と言えます。

・2マスの間に奇数本入るなら、その色は異なる。
・2マスの間に偶数本入るなら、その色は同じである。

また、対偶の真偽も一致するので、以下の命題も真です。

・2マスの色が同じであるなら、その間には偶数本入る。
・2マスの色が異なるなら、その間には奇数本入る。

証明完了

すこしはしょった部分もありますが、ざっとこんな感じです。

境界定理（仮）のメリットとデメリット

　しかし、この定理はどんな風に役立つのでしょうか。大雑把に言うと、本数定理を知覚できるようになる、ということです。

例えばヤジリンを解くときに、このような場面があったとします。

このとき、線は必ず1本通るので、ヒントマスは白マスになります。これを踏まえて、次の問題を見てみましょう。

1のマスはすべて白マスであることが分かります。また、同じ色の間には偶数本入るため、

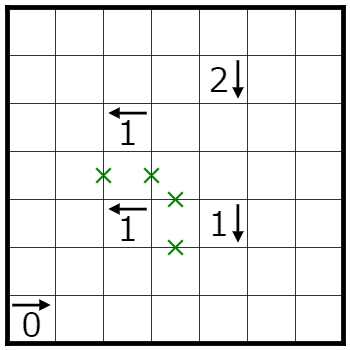
そして、線の通らないマスは黒マスになるので、

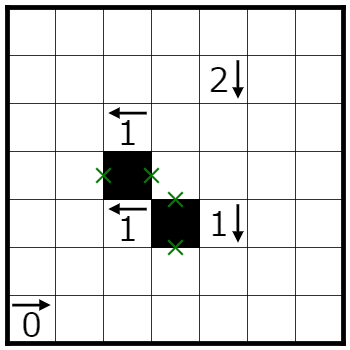
　本数定理にまだ慣れないうちはこんな考え方もアリなのかな、と思いました。

　また、デメリットとしては、使えるパズルが少ないことでしょうか。枝分かれも交差もしないループ系パズルで、しかもループの外、もしくは中にある要素が必要になるので、かなり限られると思います。

そしてもう一つ、Castle Wall の×の考え方について掘り下げたかったのですが、まだまだ時間がかかりそうなのでまた別の機会に話したいと思います。ガッカリさせて本当にごめんなさい。

さいごに

　めちゃくちゃ薄っぺらい内容になったり、結局 Castle Wall 全然語ってなかったり、色々問題がありますが、最後まで読んでくれて本当にありがとうございました。
　来年はちゃんと計画立てて参加するようにします......