
統計的因果探索
統計的因果探索の基本的な部分は既にtksさんが投稿(データから物事の原因を特定する 因果探索入門)していますのでそちらを読んて頂くと分かりやすいと思います。本稿では制約どうやって突破したら良いのかの模索について書いています。
きっかけ
弊社で因果探索をサービス化したきっかけはある製造業分野の方からの相談に始まります。
内容はこんな感じです。
「ある工程の順序や配合の組み合わせは膨大になる。あるときは全然ダメ、ある時は良い。なにが原因でよくなったり、悪くなったりするのか分からないのだろうか?」
※なんとなく意味を理解してもらえるレベルで具体的な内容をボカシています。
ご担当者は相当以前からこのことの解明に苦労していて最終的には「数社のデータ解析を依頼したがエクセルとpythonでの分析報告だった。」
「あの程度のことは自分もやってたのに、、、大金使ってもダメだった。」
と吐露しておりました。
実は私も協力したくてもどんな方法で分析すべきかわ分かっていませんでした。因果推論という方法は知っていましたが因果構造などをある程度ドメイン知識を活用して仮定する必要があったので少し無理があり、論文を漁ってみるということをしていました。
・論文のなかで使えそうなものを探す
・私がちゃんと理解できる
・私が実装可能
この条件が必須です。
幾つかを検討・検証を進めてきましたがその中でも滋賀大・清水教授のLiNGAMは平均的に最も良い結果を出すことがわかりました。
弊社では2012年頃から検討・検証を進めてきましたがLiNGAMの商用許可を滋賀大・清水教授から頂き2019年に因果探索サービスを開始しました。
今はNTech Predictの機能の一部になっています。初期の論文を元にC++でスクラッチ開発しましたが現在は清水教授のオープンプロジェクト(https://github.com/cdt15/lingam)を一部利用させて頂いています。
滋賀大・清水教授の論文
S. Shimizu, P. O. Hoyer, A. Hyv舐inen, and A. Kerminen. A linear non-gaussian acyclic model for causal discovery. Journal of Machine Learning Research, 7: 2003--2030, 2006.
LiNGAM(Linear Non-Gaussian Acyclic Model: 線形非ガウシアン非巡回モデル)
n個の観測変数Xと観測変数に影響を与えている変数で例えばノイズなどの直接観測できない要素ε

仮定1:εは互いに独立で非ガウス連続分布に従う。
注:独立性を仮定することは、各観測変数に対して、未観測共通原因がないことを意味する。
仮定2:線形性
仮定3:各観測変数の因果関係は非巡回である。これは因果グラフのどの変数から出発して関係性をたどっても、元の変数に戻って来られないことを意味します。

非ガウス分布の仮定( Non-Gaussian )
従来の因果推論は相関や2次の統計量を用いて因果の方向などを推定し、観測されていないノイズ等はガウス分布を仮定していました。しかし、ガウス分布の仮定では一般的に因果の方向などは識別不可能なことが証明されています。Pearl,2000 Spirtes at al. 2000
長らく因果の方向などは識別不可能で、出来ないと思われてきましたが、清水教授は非ガウス分布であれば因果の方向を特できることを数学的に証明し、その手法がLiNGAMとして体系されました。
おそらく厳密な表現では無いですが平たく言えば非ガウス分布=ガウス分布を除く他の分布全ての分布なので因果の方向を特定するためのデータ分布に関しては制約が少ない優れた方法です。その一方でLiNGAMには上で述べたように幾つかの仮定があります。
「仮定があるの?」、ですが何もLiNGAMだけではありません。この辺りは「仮定がある」ということを説明すると「なんだ、仮定を満たさないと使えないかぁ」という反応が返ってきますが「いままでどうやってたんですか」と聞くと「相関を出して相関係数見てますね」と返って来たります。心の中で「それって線形を仮定してるよ」と思うのですがその他にも統計では正規分布を仮定しているものは多くありますが使っている方(データサイエンティスト含めて)そこちゃんと見ている方は少ないのも実際問題としてはあります。なので「仮定」という言葉は営業的にはマイナス面を強調していることにもなるので難しいです。
上記のそれぞれの仮定が何を意味しているのかを簡単に説明しておきます。
仮定1
これはモデル(線形回帰)したときの残差が独立していないということはまだなんかの影響因子があるとみなせます。実は仮定の中でこの仮定は重要で現場で使う時に一番注しないといけないものになります。

仮定2
・(0,1や(ある、無い)、(ON,OFF)といった離散的な値があると適用出来ない。(非線形性と離散値は散布図で確認できます)
・非線形性があると適用出来ない。

仮定3
因果関係は一方向かつ自己相互作用が無いことです。原因Aの結果がBであると同時にAの原因がBであるという巡回した関係

色んな仮定、制約がありますが統計の計算上、正規分布の仮定があってもわりとそんなのは無視して適用しても問題にならない(気が付かない)場合は少なくありません。
余談ですが微分と積分は順序交換は無条件にやってはいけない行為で微積分の計算ではうるさく言われるのですが、ある数学者いわく「ふつうは黙って気にせず計算してる」ということを聞いたことがあります。
もちろん何かあったときにそこへ立ち返って訂正できる能力があることが前提で言った言葉だと思います。それと同じだと思いますのでむやみやたらにルール無視な計算をしてはいけないということは肝に銘じておくべきです。
話を戻すと非線形性、離散データが在る場合にだまってLiNGAMを適用したらどうなるのかを見てみると完全にアウト!かといえば実はそうでは無かったりします。ICA-LiNGAMは線形モデルですが実験結果から非線形データに対してもある程度正しい結果が期待できます。
※計算時間、メモリ消費量、因果グラフの正しさ等の総合的な観点からもICA-LiNGAMは非常に安定的だったという意味です。

正しいエッジ(矢印)に対して推定されたエッジの正解率
因果探索を実施する場合、非常に強い非線形性やデータの多くが離散データ等の特殊な場合を除けばLiNGAMは最初の選択肢として考えても問題無いと思います。
つまり、因果探索したかったらまずは黙ってLiNGAMでやってみるというのは現時点では悪くない選択といえます。しかし、もっとも注意しなければならないのは上でも述べたように未観測な情報があってそれが2つ以上の観測データに影響を与えている場合です。

これは利用する側からするかなり大きな問題です。
早い話、LiNGAM使うなら未観測な情報は可能な限り無くさないといけないので現実的に不可能です。
実際、そのような未観測な情報は無数にあるといっても良いと思います。それでもLiNGAMはかなり正確な因果構造を推定できることが少なくないです。これは想像ですが2つ以上の観測データに影響を与えている情報でも相応に大きな影響因子は大抵の場合は観測されていて影響が少ない因子は未観測であってもLiNGAMが誤るほどではないことがしばしばあるのではないかと思います。
現時点では全ての仮定を無くして安心して使える因果探索技術は確立されていないようですが、そういった制約を外す試みは続けられています。特に未観測の共通原因があっても適用可能な因果探索方法としてRCDという技術が開発されています。ただ、弊社の様々なケースによる実験ではLiNGAMと置き換えるほどのメリットは残念ながらありませんでした。
RCD
T. N. Maeda and S. Shimizu. RCD: Repetitive causal discovery of linear non-Gaussian acyclic models with latent confounders. In Proc. 23rd International Conference on Artificial Intelligence and Statistics (AISTATS2020), Palermo, Sicily, Italy. PMLR 108:735-745, 2020.
最大のデメリットは処理時間とサンプル数依存性です。LiNGAMではサンプル数^0.2に比例するのに対してRCDではサンプル数^2.9に比例してしまいます。

これは項目数(変数の数)でも同様な関係があります。LiNGAMではサンプル数に比例するのに対してRCDではサンプル数^3に比例してしまいます。
データ内の共通変数を削除して未観測共通変数が有る状態でのLiNGAMとRCDの計算結果では大きくRCDが勝っている結果が得られませんでした。
これについては様々な条件が仮定されている点を無視してデータを放り込んだので仕方ない結果ではありますがそれでもLiNGAMは頑健性の高さを示した結果になりました。
「LiNGAMが一番良い」といった表現に関して
誤解を招く前に少し説明しておきますと様々な手法(アルゴリズム)があり、それらは固有の前提条件(仮定)が存在しています。因果探索を一般ユーザー向けに利用してもらうことを考えるときそのようなユーザーは間違いなく何も考えずにデータを放り込んできます。(実際そうです。)
その場合の対処ですが大きく分けて4通りあると思います。
(1)固有の前提条件(仮定)をシステムがチェックしてNGならその旨のメッセージを出す。
(2)固有の前提条件(仮定)をシステムがチェックしてNGならエラーにする。
(3)固有の前提条件(仮定)が不要な因果探索を使う。
(4)固有の前提条件(仮定)が多少満たしていなくてもある程度信頼できる因果探索を使う。
(1)と(2)はおそらく理想的なデータ以外はかならずNGになります。(3)は今の所存在しないので除外、そうなると(4)の選択肢になります。
他にも選択肢を用意できると思いますが諸般の事情から除外しました。例えば開発コストとかです。
さらにどのアルゴリズムもデータ量が影響するし計算資源も影響します。計算資源の影響というのは恐ろしく高速な計算が必要とか膨大なメモリ量が必要などで一般ユーザーには到底手の届かない世界ではやはり使ってくれなくなります。
上記、諸々を考慮して見たときに「LiNGAMが一番良い」と書いていますのでご了承ください。
因果探索(LiNGAM)の仮定緩和の研究
その他の因果探索(LiNGAMの仮定の緩和)の研究としては以下の物があります。

やはり、理論(統計学、数学)としては成立してはいるが現実の問題に当てはめてみると数値計算結果としては満足できる結果には成らないことが少なくないという結果で実用上はLiNGAMが今の所最適です。
Structural Agnostic Modelling
Deep learningを使って因果探索するという試みはあります。
代表的な物としてSAM( Structural Agnostic Modelling)があります。SAMもLiNGAMと同様に線形性を仮定していることと離散値に対応していない点に注意が必要です。
Diviyan Kalainathan et.al., Structural Agnostic Modeling: Adversarial Learning of Causal Graphs
SAMは、GAN(Generative Adversarial Network:敵対的生成ネットワーク)を用いて「因果探索」を行うモデルで、粗っぽく言えばSAMは因果関係をデータ生成の順番として考えどのような順でデータが生成されたのかを推定します。生成AIに近いものとも言えます。
これも弊社の検証ではLiNGAMと置き換えるほどの成果は得られませんでした。
非線形因果探索
Autoencoder-based causal discovery based on multivariate post-nonlinear model
https://github.com/rafcc/abpnl
Deep learningを使って非線形因果探索するという試みですが弊社での検証ではやはり現実的なデータでは満足できる結果が出せませんでした。
ただし、人工的な非線形データではabpnlはLiNGAMと比べて良い結果を出しましたが処理時間がやはり無視できません。
多変数データを用いた非線形因果探索技術の開発https://www.riken.jp/press/2022/20220426_4/index.html
A Multivariate Causal Discovery based on Post-Nonlinear Model, CLeaR 2022
Estimation Of Post-Nonlinear Causal Models Using Autoencoding Structure, ICASSP 2020
個人的な独自実装
それとあくまで個人的な実験的な独自実装があります。といってもあくまで個人的な実験ではありますがDeep learningを使って非線形因果探索するという試みで post-nonlinear modelのg, f をDeep learningで直接推定してしまうという案です。ただし、残差を最小かつ残差間の独立性を最大にする制約条件を課しています。上記のabpnlに近い方法ですが未観測共通原因μの存在を仮定した計算をしています。当然μは上記の制約条件の中で最適化する必要があります。良好な結果が得られますが計算時間が許容できる限度を超えるためまったく実用的ではありません。

μは一般化ガウス分布

β、ρは未定のパラメータで最適化で推定します。未観測共通原因μで未観測な情報は寄与の小さいものを全て含めると基本的にはガウス分布に近いであろうという仮定です。これは中心極限定理から標本サイズ(サンプルサイズ)が大きくなるほど、標本平均は正規分布で近似できることを述べた定理が近似的に成立しているであろうという仮定です。ただし、ガウス分布の形からはずれる事もあるはずでそれをパラメータβ、ρで制御するという考えです。

eは残差ベクトル、MIは相互情報量
ε=0.0001 w1=0.7 w2=0.4
eは残差ベクトル、MIは相互情報量です。
lossを最小化するというこで、残差と残差間の相互情報量がともに最小になるように求めることになります。
abpnl(Autoencoder-based causal discovery based on multivariate post-nonlinear )modelでは下図のような結果になるらしい。
データセットはhttps://www.fmrib.ox.ac.uk/datasets/netsim/index.html
から入手可能です。

S. M. Smith, K. L. Miller, G. Salimi-Khorshidi, M. Webster, C. F. Beckmann, T. E. Nichols, J. D. Ramsey, and M. W. Woolrich. Network modelling methods for FMRI. NeuroImage, 54(2):875-891, 2011.
黒点線矢線が正解
赤矢線が推定結果

Estimated DAGs from fMRI simulation data sim2

データはfMRIシミュレーションデータでabpnlではx6→x7が欠落、x2→x7が逆になっている以外は全て正解しています。一方でICA-LiNGAMでは図のようになった。

lassoλ=0.2
灰色X2は残差がガウス分布になってしまった事を意味する
数値の意味としてはカッコ内は相関係数、カッコの外は因果効果(係数)

結果としてICA-LiNGAMはわりと善戦している事が分かりますが残念ながら逆向きのパスを出してしまっています。そして個人的な独自実装での結果は次のようになりました。

数値の意味としてはカッコ内は相関係数、カッコの外は Feature Importance、%値は信頼性
Feature Importanceは最大を1.0としたときの相対値

abpnlとはx6->x7、x2→x7が一致しなかったがそれ以外は一致しました。ただし、x6->x7、x2→x7は正解を示しています。

Estimated DAGs from fMRI simulation data sim1

このケースではabpnlは問題の無い解を推定しています。一方、個人的な独自実装での結果は次のようになった。


abpnlの結果と完全に一致しました。
次に明らかに非線形の人工的なデータではどうなのか?
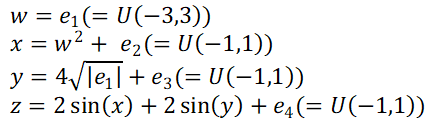

画像引用)Nonlinear causal discovery with additive noise


Feature Importanceは最大を1.0としたときの相対値

未観測共通原因μの存在を仮定しているためFeature Importanceは下図のようになっています。そのため未観測共通原因(Unknown#)が推定されてしまうことがあります。このデータでは未観測共通原因μは存在しないはずなのでUnknown#の寄与度は出て欲しくない所ですが旨く対処できていません。

推定された因果構造に対する非線形フィットは図のような感じになっていました。

この図を見てみると(3段目の図)本来存在しない x→y が絶妙にフィットされています。このためlossを引き下げてしまい存在しないパスを生成していまったと思います。
一方、ICA-LiNGAMでは以下のようになった。

lassoλ=0.2
数値の意味としてはカッコ内は相関係数、カッコの外は因果効果(係数)

やはり、結果としてICA-LiNGAMはわりと善戦している事が分かる。
この実験ではICA-LiNGAMで因果を逆向きに推定する事は無かった。
上記「冗長なエッジ」に関して
冗長なエッジと書いていますが正確な表現では無いです。正解エッジを消す事無くlasso回帰等で落とせるなら冗長なエッジですがそこは確認していません。正しくは「正解エッジには無い」という意味と考えて下さい。
正解と不正解に分ければ良いのですが逆向きは不正解としても重罪と考えたからです。
どんな因果探索アルゴリズムを使うのが良いのか?
上で述べたように因果探索を使うと言う場面においてはまずはICA-LiNGAMを黙って適用して見ると言うのは選択としてはそれほど間違っていないと言えます。
ある程度正しい因果が既知の場合はDirect-LiNGAMという選択もあります。
Direct-LiNGAMの優れている点は知識を反映できると言う点ですが、これは使い方を誤ると問題です。知識の反映は正しい因果構造は「これです」という情報をインプットとしてそれを守るように因果構造を推定します。なのでDirect-LiNGAMのアウトプットは必ず知識を反映する形で出力されます。つまり誤った先入観などによって誤った因果構造を指定していると「気づき」を逃す可能性があります。その点を注意して適用できるのであれば知識とは逆方向の因果構造を推定する事はありません。
その他の因果探索に関係する技術
現時点でもっとも信頼できる方法は、データの特性や目的に大きく依存します。以下にいくつかの一般的なガイドラインを示します。具体的な状況に応じて最適な方法は異なりますのでご注意願います。
PC Algorithmとそのバリエーション(FCIなど)
制約ベースの方法は広く使用されており、特にデータが独立性の条件を満たす場合に信頼性があります。PCアルゴリズムは計算効率が高く、FCIは潜在変数が存在する場合に有用です。
Score-based Methods
GES(Greedy Equivalence Search)などのスコアベースの方法は、データがノイズを含む場合でも堅牢な結果を提供することがあります。BICやAICなどのスコア基準を使用することで、モデルの複雑さとデータの適合度のバランスを取ります。
LiNGAM
データが非ガウス分布に従う場合には、LiNGAM(Linear Non-Gaussian Acyclic Model)が非常に有効です。これは、非ガウス性を仮定することで因果方向を一意に特定できるという利点があります。
Causal Generative Neural Networks (CGNN)
ディープラーニングを使用した方法は、複雑な非線形関係をモデル化する能力があります。CGNNは特に多変量データセットに対して強力ですが、計算資源と専門知識が必要です。
Hybrid Methods(MMHCなど)
制約ベースとスコアベースを組み合わせたハイブリッド方法は、多くの場合、堅牢性と精度のバランスが良いです。MMHC(Max-Min Hill Climbing)はその一例です。
Granger Causality
時系列データに対しては、Granger因果性が非常に有効です。これは特に経済データや金融データの解析でよく使用されます。
最適な方法を選択するためには、データの性質や研究の目的をよく考慮することが重要です。
参考資料
統計的因果探索 (機械学習プロフェッショナルシリーズ)

統計的因果探索: 領域知識とデータから 因果仮説を探索するhttps://www.jst.go.jp/kisoken/aip/result/event/jst-riken_sympo2021/pdf/shimizu.pdf
因果探索: 基本から最近の発展までを概説https://www.socialpsychology.jp/seminar/pdf/2016SS_SShimizu.pdf
NTechPredict 製品付属:NTechPredict-仕様概要_時系列予測_因果探索.pdf
S. Shimizu, P. O. Hoyer, A. Hyv舐inen, and A. Kerminen. A linear non-gaussian acyclic model for causal discovery. Journal of Machine Learning Research, 7: 2003--2030, 2006.
S. Shimizu, T. Inazumi, Y. Sogawa, A. Hyv舐inen, Y. Kawahara, T. Washio, P. O. Hoyer and K. Bollen. DirectLiNGAM: A direct method for learning a linear non-Gaussian structural equation model. Journal of Machine Learning Research, 12(Apr): 1225--1248, 2011.
Y. Zeng, S. Shimizu, H. Matsui, F. Sun. Causal discovery for linear mixed data. In Proc. First Conference on Causal Learning and Reasoning (CLeaR2022). PMLR 177, pp. 994-1009, 2022.
T. N. Maeda and S. Shimizu. RCD: Repetitive causal discovery of linear non-Gaussian acyclic models with latent confounders. In Proc. 23rd International Conference on Artificial Intelligence and Statistics (AISTATS2020), Palermo, Sicily, Italy. PMLR 108:735-745, 2020.
T. N. Maeda and S. Shimizu. Causal additive models with unobserved variables. In Proc. 37th Conference on Uncertainty in Artificial Intelligence (UAI). PMLR 161:97-106, 2021.
Diviyan Kalainathan et.al., Structural Agnostic Modeling: Adversarial Learning of Causal Graphs
A Multivariate Causal Discovery based on Post-Nonlinear Model, CLeaR 2022
Estimation Of Post-Nonlinear Causal Models Using Autoencoding Structure, ICASSP 2020
