ロジスティック回帰：概要とPythonによる実装

ロジスティック回帰とは何か？

ロジスティック回帰は、主に二値分類問題に使用される機械学習のアルゴリズムです。つまり、あるデータが2つのクラスのうちどちらに属するかを予測するための手法です。名前に「回帰」とついていますが、これは予測値が確率を表現するためです。

ロジスティック回帰の考え方

ロジスティック回帰の基本的なアイデアは、入力値の線形結合を取り、その値をロジスティック関数（またはシグモイド関数）に通すことです。このシグモイド関数の出力は0から1の間であり、それを確率として解釈します。

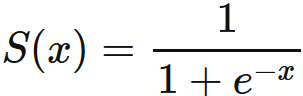
ロジスティック回帰のPythonによる実装

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

# データセットの読み込み
iris = load_iris()
X = iris.data[:, [2, 3]]
y = (iris.target !=0)

# データの分割（訓練データとテストデータ）
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# ロジスティック回帰モデルの訓練
model = LogisticRegression(max_iter=200)
model.fit(X_train, y_train)
# テストデータでの予測
y_pred = model.predict(X_test)
# 予測の精度評価
accuracy = accuracy_score(y_test, y_pred)

データの可視化

# 散布図の描画（訓練データ）
plt.figure(figsize=(10,6))
plt.scatter(X_train[y_train == 0][:, 0], X_train[y_train == 0][:, 1], color='b', label='setosa')
plt.scatter(X_train[y_train == 1][:, 0], X_train[y_train == 1][:, 1], color='r', label='others')

# 決定境界の描画
x_values = np.linspace(0, 7, 500)
y_values = -(model.intercept_[0] + np.dot(model.coef_[0][0], x_values)) / model.coef_[0][1]
plt.plot(x_values, y_values, label='decision boundary')

plt.xlabel('Petal length')
plt.ylabel('Petal width')
plt.legend()
plt.show()

上記のグラフは、2つの特徴量を持つ2クラスのデータセットに対するロジスティック回帰の結果を示しています。青色の点はクラス0のデータを、赤色の点はクラス1のデータを表しています。また、線はロジスティック回帰モデルによる決定境界を示しており、この線を境にしてクラス分類が行われます。

ロジスティック回帰の応用

ロジスティック回帰は、医療、マーケティング、金融、工学など、さまざまな分野で広く使用されています。疾患のリスク予測、顧客の購買予測、金融リスク予測、画像内の物体識別など、実世界の問題を解決するために活用されています。
ただし、ロジスティック回帰は単純なモデルであり、複雑なパターンを捉えるには限界があります。そのため、より高度な手法（例えば、ランダムフォレスト、サポートベクターマシン、ニューラルネットワークなど）が必要な場合もあります。