
Ai分布とは?地震層せん断力係数との関係【建築士試験】
こんにちは!ゼロ所長です。
今日はAi分布と地震層せん断力係数について考えるね。
こんな問題が出題されることがある。
地震層せん断力係数の建築物の地上部分における高さ方向の分布を示す係数 Ai の値は、一般に、建築物の上層ほど 小さくなる 。
正解は・・・ ×となるのだけど、なぜだかわかる?
知識ゼロの人が読んだら意味不明の文章だね。
一緒に考えてみよう。
地震層せん断力係数とは
地震層せん断力係数Ciは、建物の層に作用する地震力の割合(比率)なんだ。地震層せん断力係数は地震力に比例する。ということは、Ciが大きくなるほど地震力も大きくなるね。
地震力Qと層せん断力係数Ciには下記の関係があるよ。
Q=W×Ci
Wは建物の層のもつ重さだね。地震層せん断力係数Ciは下式で計算する!
Ci=Z×Rt×Ai×C0
それぞれの記号は下記を意味するよ。
Z:地域係数
Rt:振動特性係数
Ai:i階のせん断力分布係数(Ai分布)
C0:標準層せん断力
ややこしいね!覚えることが沢山だ。
ともかく、層せん断力係数は「色々な要因を考慮して決定する」という点は覚えてほしい。Ai分布はCiを決定する要因の1つということだね。
今回はAi分布という値が問題になっているから、今回は層せん断力係数とAi分布の関係だけを解説するね。
おっと、その前にまずは層の意味について理解しようか。
建築物の層は、言い換えれば構造的な床と考えるとわかりやすいよ。建築物の構造計算をするとき、「階」よりも「層」が重要になる。
なぜかというと、水平方向に作用する地震力は構造的な床(層)に作用するからなんだ。
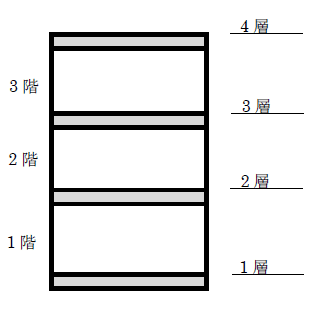
なぜ床(層)に地震力が集中するのかというと、水平力に対して「水平方向に配置された床」が最も剛性が高い(最もかたい)と仮定できるからなんだ。
物理が苦手な人向けにおさらいすると、力Pと剛性K、変形δの関係は下記となる。
P=Kδ
上記より、剛性が大きいほど作用する力も大きいとわかるよね。
そして、建物の床(層)は質点という、質量だけをもつ点に単純化して耐震設計をするのだけど・・・本筋から外れそうだから、これ以上の解説はやめておこう!

Ai分布とは
Ai分布とは地震層せん断力係数の高さ方向の分布を表す値だよ。
Ai分布はこんな難しい計算式で求めるんだ。

T:建物の設計用1次固有周期(T=h(0.02+0.01α))
αi:i階より上の部分の建物重量と、地上部分の建物重量の比
W:地上部分の建物全重量
Wi:i階より上の部分の建物重量
うーん。難しいね!
よし、できるだけ分かりやすくAi分布の式を説明してみよう。
地球には重力がある。だから物の重さは常に下向きの方向に作用するね。
ところで皆は肩車をしたことがあるかな?
肩車をすると、上に乗った人の重さが自分の身体にかかってくるね。
乗った人の体重が40kg、自分の体重が60kgだとすると、自分自身は100kgの重さを体感していることになるね!
もう1つ例題。たとえば10個の積み木を重ねたとする!
このとき、一番上に載せた積み木は一番軽くなるね。当たり前だけど。
逆に、一番下の積み木は、その上に9個の積み木が載っているから、9個分の積み木の重さがかかって、一番重くなる!

さっきの重さの話を一般化(普遍的な法則や概念を引き出すことだ!)してみよう。
・建物重量は上階にいくほど小さくなる
・下階にいくほど上階の重さが加わるので建物重量は大きくなる
上記よりαi=Wi/W、Wiの関係は

だとわかるね。もう一度Ai分布の式をみてみよう。
αが大きい値、小さい値を実際に代入してみて、Ai分布がどう変化するかみてみるんだ。Tは建物ごとに一定の値だから、Ai分布の傾向を掴むだけなら無視してもいいよ。

実際に計算すると下記のことがわかる!
・αiが大きい(下の階) ⇒ Aiは小さい
・αiが小さい(上の階) ⇒ Aiは大きい
そう。Ai分布は上の階にいくほど大きくなって、下の階になるほど小さく(1に近づく)なるよ。
建築士試験を解くだけならAi分布の形のザックリしたイメージをもっておくといいよ。こんな台形型になるはずだ。

絵や図形などのイメージを持つことは、公式を覚えてられない人におすすめだよ。
まとめ
以上より、Aiの値は、一般に、建築物の上層ほど「大きくなる」が正しい説明だとわかるね。
参考
最後に参考にした記事を掲載しておくね~。それでは~。
いいなと思ったら応援しよう!

