
曲げモーメントを解説!計算方法と公式一覧|構造力学の基礎を学ぼう
やあ、ゼロ所長だよ!
今日は「曲げモーメント」について、わかりやすく解説していこう!
構造力学の基礎だから、しっかり理解していこうね!
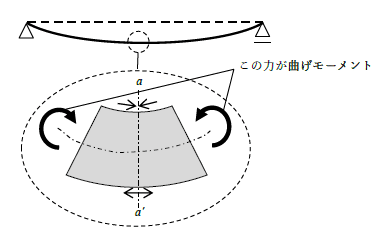
曲げモーメントとは?
曲げモーメントとは、部材を曲げようとする内部の力(応力)のことだね。
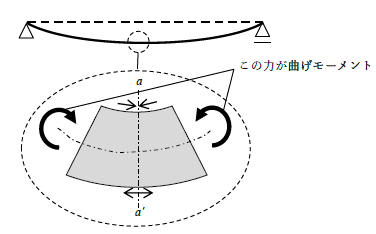
簡単に言うと、「物体を回転させようとする力」が部材の内部に発生するイメージだよ。つまり、曲げモーメントは応力の1つだ!
たとえば、本を両手で曲げてみよう!

上側が縮んで、下側が伸びるよね?
このとき、本の中には「曲げモーメント」が発生しているんだ!
つまり、曲げモーメントが作用すると、部材の断面が湾曲するんだね。
これ重要ポイントだから覚えておいてね!
勘違いしやすい例:曲げモーメントと外力モーメントは違う
もう一回いうけど、曲げモーメントは応力の1つだよ!だから、部材内部で発生する力なんだ。
勘違いしやすい点として、外力や反力として作用するモーメントは、曲げモーメントとは言わないから注意してね!

曲げモーメントは引張力と圧縮力の組合せ応力
実は、曲げモーメントって引張力と圧縮力の組合せ応力なんだ!
これはどういうことだろう?物体が「伸びる」とき物体には引張る力、物体が「縮む」とき物体を圧縮する力が生じているね。
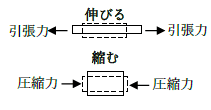
曲げモーメントが作用すると、一方は伸びてもう一方は縮むよね!

だから曲げモーメントは「引張力と圧縮力が組み合わさった応力」と言えるんだ!
ちなみに、部材断面を注意深くみると「伸びも縮むもしない断面」がある!
この面を「中立面」、中立面と断面が交わる軸を「中立軸」というよ!
曲げモーメントの記号と単位
記号:M
単位:kNm(キロニュートンメートル)やNm(ニュートンメートル)→ 建築業界では「kNm」がよく使われるよ!
実際、ゼロ所長が構造設計するときも単位はkNmを使うかな!
曲げモーメントの計算式
曲げモーメントの計算式は
支持条件
荷重条件
で変わるんだ!後で公式をのせておくから必ず目を通してね!
でも基本的な考え方は同じで
M = 力(N) × 距離(m)
を計算するよ。PLとかwL^2/2とか色々な計算式があるけど、荷重と距離を掛け算することに変わりはない!
もちろん、上式のように単純な掛け算で曲げモーメントが求められることは少ないから注意してね
曲げモーメントの正負の考え方
曲げモーメントには回転方向によって「正の値と負の値」を定義するよ!

✅ 正の曲げモーメント(下側凸)
→ 梁の上側が圧縮、下側が引張になるよ。
✅ 負の曲げモーメント(上側凸)
→ 梁の上側が引張、下側が圧縮になるね。
構造設計では、この「正負」を意識しながら計算することが重要だよ!
曲げモーメント図の書き方
曲げモーメント図を書くときのポイントを押さえよう!
部材が壊れそうな位置(=曲げモーメントが最大となる位置)をイメージする。
集中荷重がかかる場合は、曲げモーメントの分布は直線。
等分布荷重の場合は、曲げモーメントの分布は曲線になる。
集中荷重が作用する単純梁の曲げモーメント図
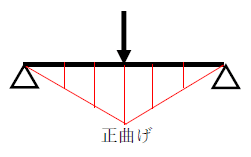

等分布荷重が作用する単純梁の曲げモーメント図

モーメント荷重が作用する単純梁の曲げモーメント図

曲げモーメントの公式一覧
曲げモーメントの公式を示しておくね!
片持ち梁の曲げモーメント
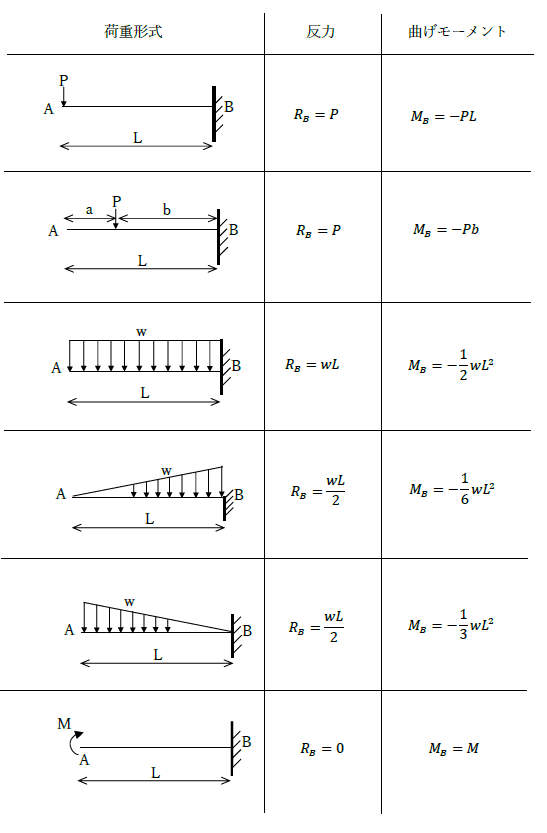
単純梁の曲げモーメント

これらの公式をしっかり押さえて、設計計算に活かそう!
まとめ
曲げモーメントは、部材を曲げようとする力(応力)!
曲げモーメントが作用すると、部材の断面が湾曲する
正負の符号を理解しよう!(下側凸は正、上側凸は負)
曲げモーメントの公式をマスターすれば、設計計算がラクになる!
「なるほど!ちょっとわかってきた!」という人は、実際に公式を使って問題を解いてみよう!
理解が深まるはずだね!
この記事が役に立ったらスキをお願いします!
参考
いいなと思ったら応援しよう!

